
【题目】综合与实践
已知,在Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕点D旋转,它的两边分别交AC,CB(或它们的延长线)于点E,F.

(1)(问题发现)
如图1,当∠EDF绕点D旋转到DE⊥AC于点E时(如图1),
①证明:△ADE≌△BDF;
②猜想:S△DEF+S△CEF= S△ABC.
(2)(类比探究)
如图2,当∠EDF绕点D旋转到DE与AC不垂直时,且点E在线段AC上,试判断S△DEF+S△CEF与S△ABC的关系,并给予证明.
(3)(拓展延伸)
如图3,当点E在线段AC的延长线上时,此时问题(2)中的结论是否成立?若成立,请给予证明;若不成立,S△DEF,S△CEF,S△ABC又有怎样的关系?(写出你的猜想,不需证明)
【答案】(1)①证明见解析;②![]() ;
;
(2)上述结论成立;理由见解析;
(3)不成立;S△DEF﹣S△CEF=![]() ;理由见解析.
;理由见解析.
【解析】
(1)①先判断出DE∥AC得出∠ADE=∠B,再用同角的余角相等判断出∠A=∠BDF,即可得出结论;②当∠EDF绕D点旋转到DE⊥AC时,四边形CEDF是正方形,边长是AC的一半,即可得出结论;
(2)成立;先判断出∠DCE=∠B,进而得出△CDE≌△BDF,即可得出结论;
(3)不成立;同(2)得:△DEC≌△DBF,得出S△DEF=![]() =S△CFE+
=S△CFE+![]() S△ABC.
S△ABC.
解:(1)①∵∠C=90°,
∴BC⊥AC,
∵DE⊥AC,
∴DE∥BC,
∴∠ADE=∠B,
∵∠EDF=90°,
∴∠ADE+∠BDF=90°,
∵DE⊥AC,
∴∠AED=90°,
∴∠A+∠ADE=90°,
∴∠A=∠BDF,
∵点D是AB的中点,
∴AD=BD,
在△ADE和△BDF中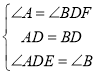 ,
,
∴△ADE≌△BDF(SAS);
②如图1中,当∠EDF绕D点旋转到DE⊥AC时,四边形CEDF是正方形.
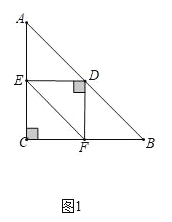
设△ABC的边长AC=BC=a,则正方形CEDF的边长为![]() a.
a.
∴S△ABC=![]() a2,S正方形DECF=(
a2,S正方形DECF=(![]() a)2=
a)2=![]() a2,
a2,
即S△DEF+S△CEF=![]() S△ABC;
S△ABC;
故答案为:![]() .
.
(2)上述结论成立;理由如下:连接CD;如图2所示:
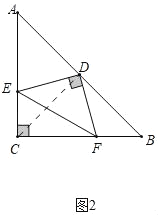
∵AC=BC,∠ACB=90°,D为AB中点,
∴∠B=45°,∠DCE=![]() ∠ACB=45°,CD⊥AB,CD=
∠ACB=45°,CD⊥AB,CD=![]() AB=BD,
AB=BD,
∴∠DCE=∠B,∠CDB=90°,
∵∠EDF=90°,
∴∠CDE=∠BDF,
在△CDE和△BDF中,
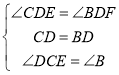 ,
,
∴△CDE≌△BDF(ASA),
∴S△DEF+S△CEF=S△ADE+S△BDF=![]() S△ABC;
S△ABC;
(3)不成立;S△DEF﹣S△CEF=![]() S△ABC;理由如下:连接CD,如图3所示:
S△ABC;理由如下:连接CD,如图3所示:

同(2)得:△DEC≌△DBF,∠DCE=∠DBF=135°
∴S△DEF=S五边形DBFEC,
=S△CFE+S△DBC,
=S△CFE+![]() S△ABC,
S△ABC,
∴S△DEF﹣S△CFE=![]() S△ABC.
S△ABC.
∴S△DEF、S△CEF、S△ABC的关系是:S△DEF﹣S△CEF=![]() S△ABC.
S△ABC.


科目:初中数学 来源: 题型:
【题目】问题探究:
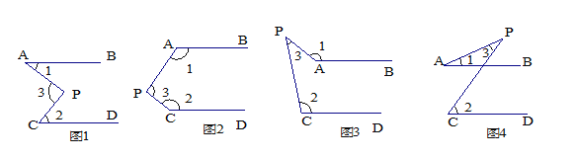
如下面四个图形中, AB∥CD.
(1)分别说出图1、图2、图3、图4中,∠1与∠2、∠3三者之间的关系.
(2)请你从中任选一个加以说明理由.
解决问题:
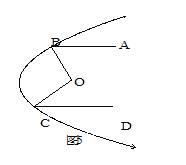
(3)如图5所示的是一探照灯灯碗的纵剖面,从位于O点的灯泡发出两束光线OB、OC经灯碗反射后平行射出.如果∠ABO=57°,∠DCO=44°,那么∠BOC=_______°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F. 
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1所示,△ABC中,∠ACB的角平分线CF与∠EAC的角平分线AD的反向延长线交于点F;
①若∠B=90°则∠F= ;
②若∠B=a,求∠F的度数(用a表示);
(2)如图2所示,若点G是CB延长线上任意一动点,连接AG,∠AGB与∠GAB的角平分线交于点H,随着点G的运动,∠F+∠H的值是否变化?若变化,请说明理由;若不变,请求出其值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=24厘米,BC=16厘米,点D为AB的中点,点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______厘米/秒时,能够在某一时刻使△BPD与△CQP全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠B=90°, AB//CD,M为BC边上的一点,AM平分∠BAD,DM平分∠ADC,
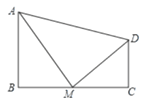
求证:(1) AM⊥DM;
(2) M为BC的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,对角线AC、BD交于点O,且分别平分∠DAB,∠ABC.
中,对角线AC、BD交于点O,且分别平分∠DAB,∠ABC.
(1)请求出∠AOB的度数,写出AD、AB、BC之间的等量关系,并给予证明.
(2)设点P为对角线AC上一点,PB=5,若AD+BC=16,四边形ABCD的面积为![]() ,求AP的长.
,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校利用五一组织老师去娄山关进行红色文化拓展活动,现有甲、乙两家旅行 社可供选择,票价都是![]() 元/人,甲旅行社的优惠方案是:按总价打八五折;乙旅行社 的优惠方案是:前
元/人,甲旅行社的优惠方案是:按总价打八五折;乙旅行社 的优惠方案是:前![]() 人按原价付费,超过的部分
人按原价付费,超过的部分![]() 折优惠.该校有教师
折优惠.该校有教师![]() 人.
人.
(1)设总价为![]() 元.写出
元.写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)在不晓得该校人数的情况下,请给学校提出比较省钱的购票建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com