
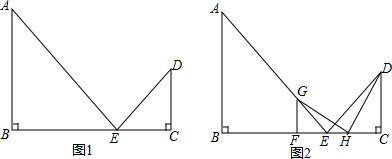
���� ��1��k=2ʱ���������֪EF=FG=2����ΪEC=CD=2������֤������EGF�ա�EDC��
��2��k=4ʱ����֪EF=FG=1�������������������CH��ֵ��
��3����֤��HG=HD�����á�HGF�ס�DHC�õ�FG=HC=$\frac{4}{k}$�����ݲ���ʽO��$\frac{4}{k}��2$���K�ķ�Χ���ɣ�
��� �⣺��1����$\frac{CE}{BE}=\frac{1}{2}$��BC=BE+EC=6��
��BE=4��EC=2��
�ߡ�EGF���EABλ�ƣ����Ʊ���1��2��
��FE=$\frac{1}{2}$BE=2��
��AB=BE��AB��BE��
���A=��AEB=45�㣬
��GF��BE��
���GFE=90�㣬
���FGE=��GEF=45�㣬
��FG=FE=2��
��EC=CD=2����C=90�㣬
��EF=FG=EC=CD����GFE=��C=90�㣬
���EGF�ա�EDC��
��2�����ڣ�
�������£�k=4ʱ����$\frac{EF}{EB}$=$\frac{1}{k}$��EB=4��
��EF=FG=1��FC=EF+EC=3��
��HC=x���ٵ�$\frac{FG}{HC}=\frac{FH}{DC}$ʱ��HGF�ס�DHC��
��$\frac{1}{x}=\frac{3-x}{2}$��
��ã�x=1��2��
x=2ʱE��H�غϲ������⣬
��x=1��
��HC=1��
�ڵ�$\frac{GF}{DC}=\frac{FH}{HC}$ʱ��HGF�ס�HDC��
��$\frac{1}{2}=\frac{3-x}{x}$��
��x=2����ʱH��E�غϲ������⣮
����������HC=1��
��3����H��E�����غϣ�
��ֻ��$\frac{FG}{HC}=\frac{FH}{DC}$ʱ��HGF�ס�DHC��
���GHF=��HDC��
�ߡ�HDC+��DHC=90�㣬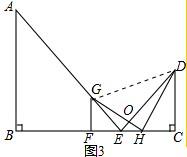
���GHF+��DHC=90�㣬
���GHD=90�㣬
�ߡ�GEO=��OHD=90�㣬��GOE=��DOH��
���GOE�ס�DOH��
��$\frac{GO}{DO}=\frac{EO}{OH}$��
��$\frac{GO}{EO}=\frac{DO}{OH}$��
�ߡ�GOD=��EOH��
���GOD�ס�EOH��
���DGO=��OEH=45�㣬
���HGD=��HDG=45�㣬
��GH=DH��
��$\frac{FG}{HC}=\frac{FH}{DC}=\frac{HG}{DH}=1$��
��FG=EF=HC��
��$\frac{EF}{EB}=\frac{1}{k}$��
��HC=EF=$\frac{4}{k}$��
�ߵ�H���߶�EC�ϣ������C����E�غϣ���
��0��HC��2��
��O��$\frac{4}{k}$��2
��K��2��
���� ���⿼��ȫ�������ε��ж������ʡ����������ε��ж������ʡ�λ�������ε����ʡ��÷��̻�ʽ��˼�������⣬������������������ǽ������Ĺؼ���
��3���С�DGH=45�Ƚǵ�֤�����Ǹ��ѵ㣬���������������ƣ����Ժ��ѧϰ��ϣ��������ã�


 ȫ�ܴ���100��ϵ�д�
ȫ�ܴ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������Ϊ���κ���y=x2-4x��ͼ��
��ͼ��������Ϊ���κ���y=x2-4x��ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����Rt��ABC�У���BAC=90�㣬AC=2AB����D��AC���е㣬��һ�����Ϊ45������ǰ���ͼ���ã�ʹ���ǰ�б�ߵ������˵�ֱ���A��D�غϣ�E��ֱ�Ƕ��㣬����EC��BE����֤��BE=CE��
��ͼ����Rt��ABC�У���BAC=90�㣬AC=2AB����D��AC���е㣬��һ�����Ϊ45������ǰ���ͼ���ã�ʹ���ǰ�б�ߵ������˵�ֱ���A��D�غϣ�E��ֱ�Ƕ��㣬����EC��BE����֤��BE=CE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ֱ��������ABC��б��AB����ֱ��l�ϣ���˳ʱ�뷽����l��ת�����Σ�ʹ��ת����A��B��C���λ���ϣ���֪BC=1����A=30�㣮��A�˶���A���λ��ʱ����A������·���ж����A������·����ֱ��l��Χ�ɵ�����ж��
��ͼ����ֱ��������ABC��б��AB����ֱ��l�ϣ���˳ʱ�뷽����l��ת�����Σ�ʹ��ת����A��B��C���λ���ϣ���֪BC=1����A=30�㣮��A�˶���A���λ��ʱ����A������·���ж����A������·����ֱ��l��Χ�ɵ�����ж���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| �༶ | �μ����� | ��λ�� | ���� | ƽ���� |
| ��3���� | 50 | 120 | 103 | 122 |
| ��5���� | 48 | 121 | 201 | 122 |
| A�� | �٢ڢ� | B�� | �٢� | C�� | �٢� | D�� | �ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
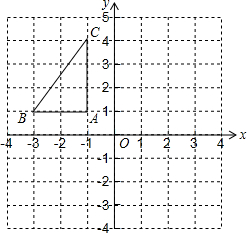 ��ͼ����ƽ��ֱ������ϵ�У���֪��ABC���������������ֱ�ΪA��-1��1����B��-3��1����C��-1��4����
��ͼ����ƽ��ֱ������ϵ�У���֪��ABC���������������ֱ�ΪA��-1��1����B��-3��1����C��-1��4�����鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com