练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．据统计2014年我国高新技术产品出口总额40570亿元，将数据40570亿用科学记数法表示为（　　）
    A．4.0570×109B．0.40570×1010C．40.570×1011D．4.0570×1012

    分析 科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．本题中40570亿，有13位整数，n=13-1=12．

    解答 解：40570亿=4057000000000=4.057×1012，
    故选D．

    点评 此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．表示时关键要正确确定a的值以及n的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    17．某渔场计划购买甲、乙两种鱼苗共6000尾，甲种鱼苗每尾0.5元，乙种鱼苗每尾0.8元．相关资料表明：甲、乙两种鱼苗的成活率分别为90%和95%．
    （1）若购买这批鱼苗共用了3600元，求甲、乙两种鱼苗各购买了多少尾？
    （2）若要使这批鱼苗的成活率不低于93%，且购买鱼苗的总费用最低，应如何选购鱼苗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．理解：数学兴趣小组在探究如何求tan15°的值，经过思考、讨论、交流，得到以下思路：
    思路一  如图1，在Rt△ABC中，∠C=90°，∠ABC=30°，延长CB至点D，使BD=BA，连接AD．设AC=1，则BD=BA=2，BC=$\sqrt{3}$．tanD=tan15°=$\frac{1}{2+\sqrt{3}}$=$\frac{2-\sqrt{3}}{（2+\sqrt{3}）（2-\sqrt{3}）}$=2-$\sqrt{3}$．
    思路二  利用科普书上的和（差）角正切公式：tan（α±β）=$\frac{tan{α}_{-}^{+}tanβ}{{1}_{+}^{-}tanαtanβ}$．假设α=60°，β=45°代入差角正切公式：tan15°=tan（60°-45°）=$\frac{tan60°-tan45°}{1+tan60°tan45°}$=$\frac{\sqrt{3}-1}{1+\sqrt{3}}$=2-$\sqrt{3}$．
    思路三  在顶角为30°的等腰三角形中，作腰上的高也可以…
    思路四  …
    请解决下列问题（上述思路仅供参考）．
    （1）类比：求出tan75°的值；
    （2）应用：如图2，某电视塔建在一座小山上，山高BC为30米，在地平面上有一点A，测得A，C两点间距离为60米，从A测得电视塔的视角（∠CAD）为45°，求这座电视塔CD的高度；
    （3）拓展：如图3，直线y=$\frac{1}{2}$x-1与双曲线y=$\frac{4}{x}$交于A，B两点，与y轴交于点C，将直线AB绕点C旋转45°后，是否仍与双曲线相交？若能，求出交点P的坐标；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列事件是必然事件的为（　　）
    A．明天太阳从西方升起
    B．掷一枚硬币，正面朝上
    C．打开电视机，正在播放“河池新闻”
    D．任意-个三角形，它的内角和等于180°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．先化简，再求值：（3-x）（3+x）+（x+1）2，其中x=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．已知点A（4，y1），B（$\sqrt{2}$，y2），C（-2，y3）都在二次函数y=（x-2）2-1的图象上，则y1、y2、y3的大小关系是y3＞y1＞y2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    19．今年江苏省参加高考的人数约为393000人，这个数据用科学记数法可表示为（　　）
    A．393×103B．3.93×103C．3.93×105D．3.93×106

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

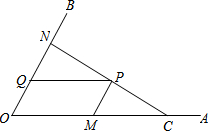    16．如图，C为∠AOB的边OA上一点，OC=6，N为边OB上异于点O的一动点，P是线段CN上一点，过点P分别作PQ∥OA交OB于点Q，PM∥OB交OA于点M．
    （1）若∠AOB=60°，OM=4，OQ=1，求证：CN⊥OB．
    （2）当点N在边OB上运动时，四边形OMPQ始终保持为菱形．
    ①问：$\frac{1}{OM}$-$\frac{1}{ON}$的值是否发生变化？如果变化，求出其取值范围；如果不变，请说明理由．
    ②设菱形OMPQ的面积为S1，△NOC的面积为S2，求$\frac{{S}_{1}}{{S}_{2}}$的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．将一副三角尺按如图方式进行摆放，∠1、∠2不一定互补的是（　　）
    A．B．
    C．D．

    查看答案和解析>>

    同步练习册答案