
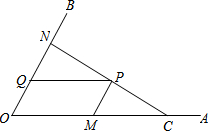
 如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.
如图,C为∠AOB的边OA上一点,OC=6,N为边OB上异于点O的一动点,P是线段CN上一点,过点P分别作PQ∥OA交OB于点Q,PM∥OB交OA于点M.分析 (1)过P作PE⊥OA于E,利用两组对边平行的四边形为平行四边形得到OMPQ为平行四边形,利用平行四边形的对边相等,对角相等得到PM=OQ=1,∠PME=∠AOB=60°,进而求出PE与ME的长,得到CE的长,求出tan∠PCE的值,利用特殊角的三角函数值求出∠PCE的度数,得到PM于NC垂直,而PM与ON平行,即可得到CN与OB垂直;
(2)$\frac{1}{OM}$-$\frac{1}{ON}$的值不发生变化,理由如下:设OM=x,ON=y,根据OMPQ为菱形,得到PM=PQ=OQ=x,QN=y-x,根据平行得到三角形NQP与三角形NOC相似,由相似得比例即可确定出所求式子的值;
②过P作PE⊥OA于E,过N作NF⊥OA于F,表示出菱形OMPQ的面积为S1,△NOC的面积为S2,得到$\frac{{S}_{1}}{{S}_{2}}$,由PM与OB平行,得到三角形CPM与三角形CNO相似,由相似得比例求出所求式子$\frac{{S}_{1}}{{S}_{2}}$的范围即可.
解答 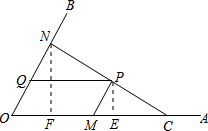 解:(1)过P作PE⊥OA于E,
解:(1)过P作PE⊥OA于E,
∵PQ∥OA,PM∥OB,
∴四边形OMPQ为平行四边形,
∴PM=OQ=1,∠PME=∠AOB=60°,
∴PE=PM•sin60°=$\frac{\sqrt{3}}{2}$,ME=$\frac{1}{2}$,
∴CE=OC-OM-ME=$\frac{3}{2}$,
∴tan∠PCE=$\frac{PE}{CE}$=$\frac{\sqrt{3}}{3}$,
∴∠PCE=30°,
∴∠CPM=90°,
又∵PM∥OB,
∴∠CNO=∠CPM=90°,
则CN⊥OB;
(2)①$\frac{1}{OM}$-$\frac{1}{ON}$的值不发生变化,理由如下:
设OM=x,ON=y,
∵四边形OMPQ为菱形,
∴OQ=QP=OM=x,NQ=y-x,
∵PQ∥OA,
∴∠NQP=∠O,
又∵∠QNP=∠ONC,
∴△NQP∽△NOC,
∴$\frac{QP}{OC}$=$\frac{NQ}{ON}$,即$\frac{x}{6}$=$\frac{y-x}{y}$,
∴6y-6x=xy.两边都除以6xy,得$\frac{1}{x}$-$\frac{1}{y}$=$\frac{1}{6}$,即$\frac{1}{OM}$-$\frac{1}{ON}$=$\frac{1}{6}$.
②过P作PE⊥OA于E,过N作NF⊥OA于F,
则S1=OM•PE,S2=$\frac{1}{2}$OC•NF,
∴$\frac{{S}_{1}}{{S}_{2}}$=$\frac{x•PE}{3NF}$.
∵PM∥OB,
∴∠PMC=∠O,
又∵∠PCM=∠NCO,
∴△CPM∽△CNO,
∴$\frac{PE}{NF}$=$\frac{CM}{CO}$=$\frac{6-x}{6}$,
∴$\frac{{S}_{1}}{{S}_{2}}$=$\frac{x(6-x)}{18}$=-$\frac{1}{18}$(x-3)2+$\frac{1}{2}$,
∵0<x<6,
则根据二次函数的图象可知,0<$\frac{{S}_{1}}{{S}_{2}}$≤$\frac{1}{2}$.
点评 此题属于相似形综合题,涉及的知识有:相似三角形的判定与性质,二次函数的性质,平行四边形的判定与性质,以及菱形的性质,熟练掌握相似三角形的判定与性质是解本题的关键.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4.0570×109 | B. | 0.40570×1010 | C. | 40.570×1011 | D. | 4.0570×1012 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
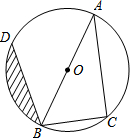 已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.(1)求BD的长;
已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.(1)求BD的长;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
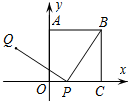 如图,正方形OABC的一个顶点O是平面直角坐标系的原点,顶点A,C分别在y轴和x轴上,P为边OC上的一个动点,且PQ⊥BP,PQ=BP,当点P从点C运动到点O时,可知点Q始终在某函数图象上运动,则其函数图象是( )
如图,正方形OABC的一个顶点O是平面直角坐标系的原点,顶点A,C分别在y轴和x轴上,P为边OC上的一个动点,且PQ⊥BP,PQ=BP,当点P从点C运动到点O时,可知点Q始终在某函数图象上运动,则其函数图象是( )| A. | 线段 | B. | 圆弧 | C. | 双曲线的一部分 | D. | 抛物线的一部分 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com