
| a2+b2 |
| a2+1 |
| b2+4 |
科目:初中数学 来源: 题型:
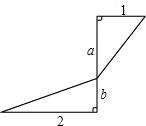
 式子
式子| a2+b2 |
| a2+1 |
| b2+4 |
| 13 |
| 13 |
查看答案和解析>>
科目:初中数学 来源:课堂三级讲练数学九年级(上) 题型:022
对于算式8a3÷a2,小明是这样理解的:求底面积为a2,体积为8a3的长方体的高是多少?你还可以理解为________.
查看答案和解析>>
科目:初中数学 来源:101网校同步练习 初三数学 人教版(新课标2004年初审) 人教实验版 题型:044
数学家高斯在上小学的时候,就曾快速地计算出了从1~100的连续整数的和,全体同学及老师无不惊叹万分,你知道高斯使用的方法吗?
现在同学们在计算这100个数字之和的时候,实际上也经常采用高斯求和法,即1+2+3+…+99+100=(1+100)+(2+99)+(3+98)+…+(50+51)=101×50=5050,另外,也还有类似的计算为:1+2+3+…+98+99+100①倒过来写:100+99+98+…+3+2+1 ②
①+②得1+2+3+…+98+99+100=10100÷2=5050.
以上两种作法,显然都可以理解为对称位置上放置了这些数字,含其中的1和100,2和99,3和98,…为对称数字,则对称数字之和均为101,继而得出结论5050,通过上述数学式子的解释,请观察下图方阵中的数字,试计算这25个数字的和.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com