
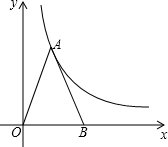
 如图,△ABO的面积为3,且AO=AB,反比例函数y=$\frac{k}{x}$的图象经过点A,则k的值为3.
如图,△ABO的面积为3,且AO=AB,反比例函数y=$\frac{k}{x}$的图象经过点A,则k的值为3. 分析 过点A作OB的垂线,垂足为点C,根据等腰三角形的性质得OC=BC,再根据三角形的面积公式得到$\frac{1}{2}$OB•AC=3,易得OC•AC=3,设A点坐标为(x,y),即可得到k=xy=OC•AC=3.
解答 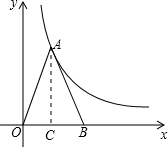 解:过点A作OB的垂线,垂足为点C,如图,
解:过点A作OB的垂线,垂足为点C,如图,
∵AO=AB,
∴OC=BC=$\frac{1}{2}$OB,
∵△ABO的面积为3,
∴$\frac{1}{2}$OB•AC=3,
∴OC•AC=3.
设A点坐标为(x,y),而点A在反比例函数y=$\frac{k}{x}$(k>0)的图象上,
∴k=xy=OC•AC=3.
故答案为:3.
点评 本题考查的是反比例函数比例系数k的几何意义:在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变.同时考查了等腰三角形的性质,反比例函数图象上点的坐标特征.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 波长(m) | 300 | 500 | 600 | 1000 | 1500 |
| 频率(kHz) | 1000 | 600 | 500 | 300 | 200 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com