
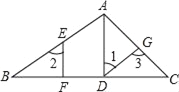
【题目】如图,在△ABC中,AD⊥BC,垂足为D,点E在AB上,EF⊥BC,垂足为F.
(1)AD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠BAC的度数.
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:
①DF=CF;
②BF⊥EN;
③△BEN是等边三角形;
④S△BEF=3S△DEF .
其中,将正确结论的序号全部选对的是( )
A.①②③
B.①②④
C.②③④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
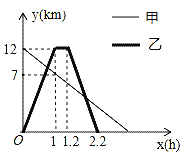
【题目】某地植物园从正门到侧门有一条小路,甲徒步从正门出发匀速走向侧门,乙与甲同时出发,骑自行车从侧门匀速前往正门到达正门后休息0.2小时,然后按原路原速匀速返回侧门,图中折线分别表示甲、乙到侧门的距离y(km)与出发时间x(h)之间的函数关系图象,根据图象信息解答下列问题:
(1)求甲到侧门的距离y与x之间的函数关系式;
(2)求甲、乙第一次相遇时到侧门的距离.
(3)求甲、乙第二次相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量江两岸码头B、D之间的距离,从山坡上高度为50米的A处测得码头B的仰角∠EAB为15°,码头D的仰角∠EAD为45°,点C在线段BD的延长线上,AC⊥BC,垂足为C,求码头B、D的距离(结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形DOE的半径为3,边长为 ![]() 的菱形OABC的顶点A,C,B分别在OD,OE,
的菱形OABC的顶点A,C,B分别在OD,OE, ![]() 上,若把扇形DOE围成一个圆锥,则此圆锥的高为( )
上,若把扇形DOE围成一个圆锥,则此圆锥的高为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+2x+a﹣2=0.
(1)若该方程有两个不相等的实数根,求实数a的取值范围;
(2)设方程两根为x1 , x2是否存在实数a,使 ![]() ?若存在求出实数a,若不存在,请说明理由.
?若存在求出实数a,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE.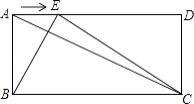
(1)若a=5,sin∠ACB= ![]() ,求b.
,求b.
(2)若a=5,b=10当BE⊥AC时,求出此时AE的长.
(3)设AE=x,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程:
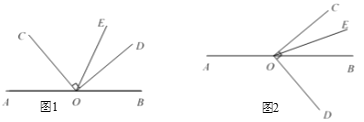
O是直线AB上一点,∠COD = 90°,OE平分∠BOC.
(1)如图1,若∠ AOC = 50°,求∠DOE的度数;
解:∵O是直线AB上一点,
∴∠AOC +∠BOC =180°.
∵∠AOC =50°,
∴∠BOC =130°.
∵OE平分∠BOC(已知),
∴∠COE =![]() ∠BOC ( ).
∠BOC ( ).
∴∠COE = °.
∵∠COD = 90°,∠DOE =∠ ∠ ,
∴∠DOE = °.
(2)将图1中∠ COD按顺时针方向转至图2所示的位置,OE仍然平分∠BOC.试猜想∠AOC与∠DOE的度数之间的关系为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字﹣2,﹣1,1,4的小球,它们的形状、大小、质地等完全相同,小强先从盒子里随机取出一个小球,记下数字为a;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为b.
(1)用列表法或画树状图表示出(a,b)的所有可能出现的结果;
(2)求小强、小华各取一次小球所确定的点(a,b)落在二次函数y=x2的图象上的概率;
(3)求小强、小华各取一次小球所确定的数a,b满足直线y=ax+b经过一、二、三象限的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com