
【题目】如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE.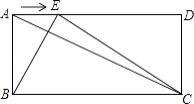
(1)若a=5,sin∠ACB= ![]() ,求b.
,求b.
(2)若a=5,b=10当BE⊥AC时,求出此时AE的长.
(3)设AE=x,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值.
【答案】
(1)解:∵四边形ABCD是矩形,
∴∠ABC=90°,
∵AB=a=5,sin∠ACB= ![]() ,
,
∴ ![]() ,
,
∴AC=13,
∴BC= ![]() =12,
=12,
∴b=12
(2)解:如图1,
∵BE⊥AC,
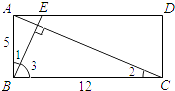
∴∠2+∠3=90°,
又∠1+∠3=90°,
∴∠1=∠2,
又∠BAE=∠ABC=90°,
∴△AEB∽△BAC,
∴ ![]() ,
,
即 ![]() ,
,
∴ ![]()
(3)解:∵点E在线段AD上的任一点,且不与A、D重合,
∴当△ABE与△BCE相似时,则∠BEC=90°
所以当△BAE∽△CEB(如图2)
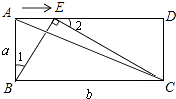
则∠1=∠BCE,
又BC∥AD,
∴∠2=∠BCE,
∴∠1=∠2, 。
又∠BAE=∠EDC=90°,
∴△BAE∽△EDC,
∴ ![]() ,
,
即 ![]() ,
,
∴x2﹣bx+a2=0,
即
![]() ,
,
当b2﹣4a2≥0,
∵a>0,b>0,
∴b≥2a,
即b≥2a时, ![]() ,
,
综上所述:当a、b满足条件b=2a时△BAE∽△CEB,此时 ![]() (或x=a);
(或x=a);
当a、b满足条件b>2a时△BAE∽△CEB,此时 ![]()
【解析】(1)根据矩形的性质得出∠ABC=90°,根据正弦三角函数得出AC,然后利用勾股定理得出BC的长,从而得出答案;
(2)根据同角的余角相等得出∠1=∠2,又∠BAE=∠ABC=90°,从而判断出△AEB∽△BAC,根据相似三角形对应边成比例得出答案;
(3)点E在线段AD上的任一点,且不与A、D重合,当△ABE与△BCE相似时,则∠BEC=90°,所以当△BAE∽△CEB(如图2),根据相似三角形的性质得出∠1=∠BCE,根据平行线的性质得出∠2=∠BCE,由等量代换得出∠1=∠2,又∠BAE=∠EDC=90°,从而判断出△BAE∽△EDC,根据相似三角形对应边成比例得出方程x2﹣bx+a2=0,将方程变形( x ![]() ) 2 =
) 2 =![]() ,当b2﹣4a2≥0,a>0,b>0,故b≥2a,综上所述得出结论
,当b2﹣4a2≥0,a>0,b>0,故b≥2a,综上所述得出结论
【考点精析】关于本题考查的矩形的性质和相似三角形的判定与性质,需要了解矩形的四个角都是直角,矩形的对角线相等;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】在2013年“崇左市初中毕业升学体育考试”测试中,参加男子掷实心球的10名考生的成绩记录如下(单位:米):7.5、6.5、8.2、7.8、8.8、8.2、8.6、8.2、8.5、9.5,则该组数据的众数、中位数、平均数依次分别是( )
A.8.2、8.0、7.5
B.8.2、8.5、8.1
C.8.2、8.2、8.15
D.8.2、8.2、8.18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州享有“中国笔都”之称,其产品畅销全球,某制笔企业欲将n件产品运往A,B,C三地销售,要求运往C地的件数是运往A地件数的2倍,各地的运费如图所示.设安排x件产品运往A地. 
(1)当n=200时,①根据信息填表:
A地 | B地 | C地 | 合计 | |
产品件数(件) | x | 2x | 200 | |
运费(元) | 30x |
②若运往B地的件数不多于运往C地的件数,总运费不超过4000元,则有哪几种运输方案?
(2)若总运费为5800元,求n的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
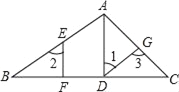
【题目】如图,在△ABC中,AD⊥BC,垂足为D,点E在AB上,EF⊥BC,垂足为F.
(1)AD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△AOD是等腰直角三角形,AB=AC,AO=AD,∠BAC=∠OAD=90°,点O是△ABC内的一点,∠BOC=130°.
(1)求证:OB=DC;
(2)求∠DCO的大小;
(3)设∠AOB=α,那么当α为多少度时,△COD是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划购买甲、乙两种图书作为“校园读书节”的奖品,已知甲种图书的单价比乙种图书的单价多10元,且购买3本甲种图书和2本乙种图书共需花费130元
(1)甲、乙两种图书的单价分别为多少元?
(2)学校计划购买这两种图书共50本,且投入总经费不超过1200元,则最多可以购买甲种图书多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在AB上,在下列四个条件中:①∠ACD=∠B;②∠ADC=∠ACB;③AC2=ADAB;④ABCD=ADCB,能满足△ADC与△ACB相似的条件是( )
A.①、②、③
B.①、③、④
C.②、③、④
D.①、②、④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年暑假,某旅行社组织了一个中学生“夏令营”活动,共有253名中学生报名参加,打算选租甲、乙两种客车载客到指定地点.甲客车2辆、乙客车1辆可坐110人,甲客车3辆、乙客车2辆可坐180人.旅行前,旅行社每辆车安排了一名带队老师,因此一共安排了7名带队老师.
(1)甲、乙两种客车各可坐多少人?
(2)请帮助旅行社设计租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】研学活动继承和发展了我国传统游学“读万卷书,行万里路”的教育理念和人文精神,成为教育的新内容和新方式.朝阳区一所中学组织学生去某市进行研学活动,原计划乘坐特快列车前往,为了节省时间,现改为乘坐高铁列车前往.已知北京与该市的距离约为1200千米,高铁列车的平均速度是特快列车的平均速度的2.4倍,且乘坐高铁列车所用时间比乘坐特快列车所用时间少用7小时,求特快列车的平均速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com