
【题目】如图,在△ABC中,点D在AB上,在下列四个条件中:①∠ACD=∠B;②∠ADC=∠ACB;③AC2=ADAB;④ABCD=ADCB,能满足△ADC与△ACB相似的条件是( )
A.①、②、③
B.①、③、④
C.②、③、④
D.①、②、④
【答案】A
【解析】解:∵∠A是公共角,
∴当∠ACD=∠B时,△ADC∽△ACB(有两组角对应相等的两个三角形相似);
当∠ADC=∠ACB时,△ADC∽△ACB(有两组角对应相等的两个三角形相似);
当AC2=ADAB时,即 ![]() ,△ADC∽△ACB(两组对应边的比相等且夹角对应相等的两个三角形相似).
,△ADC∽△ACB(两组对应边的比相等且夹角对应相等的两个三角形相似).
当ABCD=ADCB,即 ![]() 时,∠A不是夹角,则不能判定△ADC与△ACB相似;
时,∠A不是夹角,则不能判定△ADC与△ACB相似;
∴能够判定△ABC与△ACD相似的条件是:①②③.
所以答案是:A.
【考点精析】利用相似三角形的判定对题目进行判断即可得到答案,需要熟知相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).


科目:初中数学 来源: 题型:
【题目】如图,在方格纸中,每个小方格都是边长为1cm的正方形,△ABC的三个顶点都在格点上,将△ABC绕点O逆时针旋转90°后得到△A′B′C′(其中A、B、C的对应点分别为A′,B′,C′,则点B在旋转过程中所经过的路线的长是cm.(结果保留π)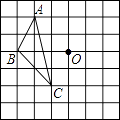
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形DOE的半径为3,边长为 ![]() 的菱形OABC的顶点A,C,B分别在OD,OE,
的菱形OABC的顶点A,C,B分别在OD,OE, ![]() 上,若把扇形DOE围成一个圆锥,则此圆锥的高为( )
上,若把扇形DOE围成一个圆锥,则此圆锥的高为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE.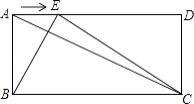
(1)若a=5,sin∠ACB= ![]() ,求b.
,求b.
(2)若a=5,b=10当BE⊥AC时,求出此时AE的长.
(3)设AE=x,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() +(﹣1)2017﹣(
+(﹣1)2017﹣(![]() ﹣
﹣![]() ),
),
(2)2(3a2b﹣2ab2)﹣3(ab2+2a2b),
(3)﹣7x2y﹣3xy2+5x2y+13xy,其中x=﹣![]() ,y=
,y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程:
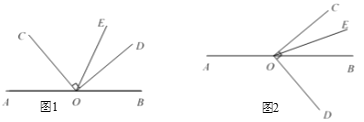
O是直线AB上一点,∠COD = 90°,OE平分∠BOC.
(1)如图1,若∠ AOC = 50°,求∠DOE的度数;
解:∵O是直线AB上一点,
∴∠AOC +∠BOC =180°.
∵∠AOC =50°,
∴∠BOC =130°.
∵OE平分∠BOC(已知),
∴∠COE =![]() ∠BOC ( ).
∠BOC ( ).
∴∠COE = °.
∵∠COD = 90°,∠DOE =∠ ∠ ,
∴∠DOE = °.
(2)将图1中∠ COD按顺时针方向转至图2所示的位置,OE仍然平分∠BOC.试猜想∠AOC与∠DOE的度数之间的关系为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
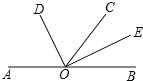
【题目】如图,点A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)当∠BOE=25°时,求∠AOD的度数
(2)在图中找出∠COD的补角,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,AB=6,BC=8,E,F分别是AB,BC的中点,AF与DE相交于I,与BD相交于H,则四边形BEIH的面积为( )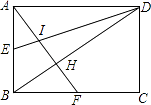
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售同一品牌羽绒服和防寒服,已知去年12月份,销售羽绒服a件,防寒服销量是羽绒服的4倍,其中防寒服售价为b元/件,羽绒服的售价是防寒服的4倍,受市场影响,今年1月份,羽绒服销量和售价均下降m%,但防寒服销量和售价均增加m%.
(1)求该商场今年1月份销售羽绒服和防寒服的销售额;
(2)若a=100,b=300,m=5,则该商场今年1月份销售羽绒服和防寒服的销售额是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com