
【题目】如图,扇形DOE的半径为3,边长为 ![]() 的菱形OABC的顶点A,C,B分别在OD,OE,
的菱形OABC的顶点A,C,B分别在OD,OE, ![]() 上,若把扇形DOE围成一个圆锥,则此圆锥的高为( )
上,若把扇形DOE围成一个圆锥,则此圆锥的高为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:连接OB,AC,BO与AC相交于点F, 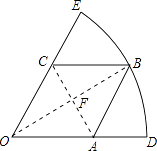
∵在菱形OABC中,AC⊥BO,CF=AF,FO=BF,∠COB=∠BOA,
又∵扇形DOE的半径为3,
∴FO=BF=1.5,
∵菱形OABC的边长为 ![]() ,
,
cos∠FOC= ![]() =
= ![]() =
= ![]() ,
,
∴∠FOC=30°,
∴∠EOD=2×30°=60°,
∴ ![]() =
= ![]() =π,
=π,
底面圆的周长为:2πr=π,
解得:r= ![]() ,圆锥母线为:3,
,圆锥母线为:3,
则此圆锥的高为: ![]() =
= ![]() ,
,
故选:D.
连接OB,AC,BO与AC相交于点F,首先利用菱形的性质以及利用三角函数关系得出∠FOC=30°,进而得出底面圆锥的周长,即可得出底面圆的半径和母线长,利用勾股定理得出圆锥的高即可.


科目:初中数学 来源: 题型:
【题目】水源村在今年退耕还林活动中,计划植树200亩,全村在完成植树40亩后,某环保组织加入村民植树活动,并且该环保组织植树的速度是全村植树速度的1.5倍,整个植树过程共用了13天完成.
(1)全村每天植树多少亩?
(2)如果全村植树每天需2000元工钱,环保组织是义务植树,因此实际工钱比计划节约多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,MN、EF分别表示两个互相平行的镜面,一束光线AB照射到镜面MN上,反射光线为BC,此时∠1=∠2;光线BC经过镜面EF反射后的光线为CD,此时∠3=∠4.试判断AB与CD的位置关系,你是如何思考的?
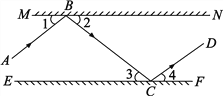
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州享有“中国笔都”之称,其产品畅销全球,某制笔企业欲将n件产品运往A,B,C三地销售,要求运往C地的件数是运往A地件数的2倍,各地的运费如图所示.设安排x件产品运往A地. 
(1)当n=200时,①根据信息填表:
A地 | B地 | C地 | 合计 | |
产品件数(件) | x | 2x | 200 | |
运费(元) | 30x |
②若运往B地的件数不多于运往C地的件数,总运费不超过4000元,则有哪几种运输方案?
(2)若总运费为5800元,求n的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图1,△ABC中,BA=BC,D是平面内不与A、B、C重合的任意一点,∠ABC=∠DBE,BD=BE. 
(1)求证:△ABD≌△CBE;
(2)如图2,当点D是△ABC的外接圆圆心时,请判断四边形BDCE的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
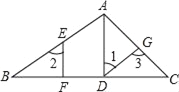
【题目】如图,在△ABC中,AD⊥BC,垂足为D,点E在AB上,EF⊥BC,垂足为F.
(1)AD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△AOD是等腰直角三角形,AB=AC,AO=AD,∠BAC=∠OAD=90°,点O是△ABC内的一点,∠BOC=130°.
(1)求证:OB=DC;
(2)求∠DCO的大小;
(3)设∠AOB=α,那么当α为多少度时,△COD是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在AB上,在下列四个条件中:①∠ACD=∠B;②∠ADC=∠ACB;③AC2=ADAB;④ABCD=ADCB,能满足△ADC与△ACB相似的条件是( )
A.①、②、③
B.①、③、④
C.②、③、④
D.①、②、④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,3).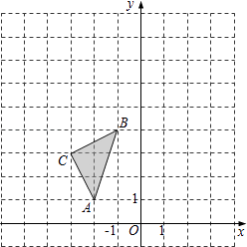
(1)画出△ABC关于y轴对称的△A1B1C1 , 并写出A1点的坐标及sin∠B1A1C1的值;
以原点O为位似中心,位似比为1:2,在y轴的左侧,画出 将△ABC放大后的△A2B2C2 , 并写出A2点的坐标;
(2)若点D(a,b)在线段AB上,直接写出经过(2)的变化后点D的对应点D2的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com