
【题目】去年暑假,某旅行社组织了一个中学生“夏令营”活动,共有253名中学生报名参加,打算选租甲、乙两种客车载客到指定地点.甲客车2辆、乙客车1辆可坐110人,甲客车3辆、乙客车2辆可坐180人.旅行前,旅行社每辆车安排了一名带队老师,因此一共安排了7名带队老师.
(1)甲、乙两种客车各可坐多少人?
(2)请帮助旅行社设计租车方案.
【答案】(1)甲、乙两种客车分别可坐40人、30人;(2)有三种租车方案:租甲种客车5辆,租乙种客车2辆;租甲种客车6辆,租乙种客车1辆,租甲种客车7辆,租乙种客车0辆.
【解析】
(1)设甲、乙两种客车可分别坐x人,y人,利用甲客车2辆、乙客车1辆可坐110人;甲客车3辆、乙客车2辆可坐180人列两个方程组成方程组,然后解方程组即可;
(2)设租甲种客车a辆,则租乙种客车(7-a)辆,利用乘车人数不少于253+7列不等式得到40a+30(7-a)≥253+7,再解不等式得到a≥5,加上a≤7,于是可得到a=5、6、7,然后写出三个方案.
(1)设甲、乙两种客车可分别坐x人,y人,
根据题意,得![]() ,
,
解得![]() ,
,
答:甲、乙两种客车分别可坐40人、30人;
(2)设租甲种客车a辆,则租乙种客车(7-a)辆,
根据题意得40a+30(7-a)≥253+7,
解得a≥5,
所以5≤a≤7,
而a为整数,
所以a=5、6、7,
有三种租车方案:租甲种客车5辆,租乙种客车2辆;租甲种客车6辆,租乙种客车1辆,租甲种客车7辆,租乙种客车0辆,


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
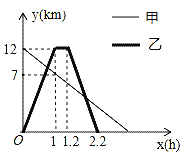
【题目】某地植物园从正门到侧门有一条小路,甲徒步从正门出发匀速走向侧门,乙与甲同时出发,骑自行车从侧门匀速前往正门到达正门后休息0.2小时,然后按原路原速匀速返回侧门,图中折线分别表示甲、乙到侧门的距离y(km)与出发时间x(h)之间的函数关系图象,根据图象信息解答下列问题:
(1)求甲到侧门的距离y与x之间的函数关系式;
(2)求甲、乙第一次相遇时到侧门的距离.
(3)求甲、乙第二次相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE.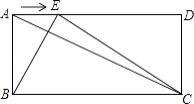
(1)若a=5,sin∠ACB= ![]() ,求b.
,求b.
(2)若a=5,b=10当BE⊥AC时,求出此时AE的长.
(3)设AE=x,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程:
O是直线AB上一点,∠COD = 90°,OE平分∠BOC.
(1)如图1,若∠ AOC = 50°,求∠DOE的度数;
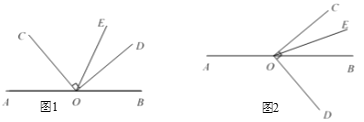
解:∵O是直线AB上一点,
∴∠AOC +∠BOC =180°.
∵∠AOC =50°,
∴∠BOC =130°.
∵OE平分∠BOC(已知),
∴∠COE =![]() ∠BOC ( ).
∠BOC ( ).
∴∠COE = °.
∵∠COD = 90°,∠DOE =∠ ∠ ,
∴∠DOE = °.
(2)将图1中∠ COD按顺时针方向转至图2所示的位置,OE仍然平分∠BOC.试猜想∠AOC与∠DOE的度数之间的关系为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
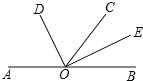
【题目】如图,点A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)当∠BOE=25°时,求∠AOD的度数
(2)在图中找出∠COD的补角,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线DE交AC于D,交AB于E.下列结论错误的是( )
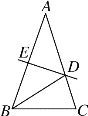
A. BD平分∠ABC B. △BCD的周长等于AB+BC
C. AD=BD=BC D. 点D是线段AC的中点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,AB=6,BC=8,E,F分别是AB,BC的中点,AF与DE相交于I,与BD相交于H,则四边形BEIH的面积为( )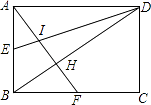
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有四个分别标有数字﹣2,﹣1,1,4的小球,它们的形状、大小、质地等完全相同,小强先从盒子里随机取出一个小球,记下数字为a;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为b.
(1)用列表法或画树状图表示出(a,b)的所有可能出现的结果;
(2)求小强、小华各取一次小球所确定的点(a,b)落在二次函数y=x2的图象上的概率;
(3)求小强、小华各取一次小球所确定的数a,b满足直线y=ax+b经过一、二、三象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的长为( )
A.![]()
B.![]()
C.4
D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com