
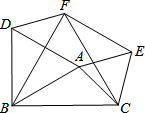
 如图,在△ABC中,AB=2,AC=$\sqrt{2}$,∠BAC=105°,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为2.
如图,在△ABC中,AB=2,AC=$\sqrt{2}$,∠BAC=105°,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为2. 分析 根据题中的等式关系可推出两组对边分别相等,从而可判断四边形AEFD为平行四边形,求出∠DAE=135°,故易求∠FDA=45°,所以由平行四边形的面积公式即可解答.
解答 解:∵△ABD,△ACE都是等边三角形,
∴∠DAB=∠EAC=60°,
∵∠BAC=105°,
∴∠DAE=135°,
∵△ABD和△FBC都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC.
在△ABC与△DBF中,
$\left\{\begin{array}{l}{BD=BA}\\{∠DBF=∠ABC}\\{BF=BC}\end{array}\right.$
∴△ABC≌△DBF(SAS),
∴AC=DF=AE=$\sqrt{2}$,
同理可证△ABC≌△EFC,
∴AB=EF=AD=2,
∴四边形DAEF是平行四边形(两组对边分别相等的四边形是平行四边形).
∴∠FDA=180°-∠DAE=45°,
∴S?AEFD=AD•(DF•sin45°)=2×($\sqrt{2}$×$\frac{\sqrt{2}}{2}$)=2.
即四边形AEFD的面积是2,
故答案为:2.
点评 本题综合考查了勾股定理的逆定理,平行四边形的判定与性质,全等三角形的判定与性质以及等边三角形的性质.综合性比较强,难度较大,有利于培养学生综合运用知识进行推理和计算的能力.


科目:初中数学 来源: 题型:选择题
| A. | m3•m2=m6 | B. | (xy)8÷(xy)4=(xy)2 | ||
| C. | a10÷(a7÷a2)=a5 | D. | x4m+x2n•x2n=1(n为正整数) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,AB是⊙O的直径且AB=4$\sqrt{3}$,点C是OA的中点,过点C作CD⊥AB交⊙O于D点,点E是⊙O上一点,连接DE,AE交DC的延长线于点F,则AE•AF的值为12.
如图,AB是⊙O的直径且AB=4$\sqrt{3}$,点C是OA的中点,过点C作CD⊥AB交⊙O于D点,点E是⊙O上一点,连接DE,AE交DC的延长线于点F,则AE•AF的值为12.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,线段AB的长为5,C为线段AB上一动点(与点A、B不重合),分别以AC、BC为斜边在AB的同侧作等腰直角三角形ACD和BCE,若AD=x,BE=y,那么x2+y2最小值是$\frac{25}{4}$.
如图,线段AB的长为5,C为线段AB上一动点(与点A、B不重合),分别以AC、BC为斜边在AB的同侧作等腰直角三角形ACD和BCE,若AD=x,BE=y,那么x2+y2最小值是$\frac{25}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在正方形ABCD中,点E,F分别在AB,BC上,且AE=CF,BE=2AE,连接DE,FG⊥DE,垂足为点G,连接CG,则tan∠FGC的值是$\frac{1}{3}$.
如图,在正方形ABCD中,点E,F分别在AB,BC上,且AE=CF,BE=2AE,连接DE,FG⊥DE,垂足为点G,连接CG,则tan∠FGC的值是$\frac{1}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com