
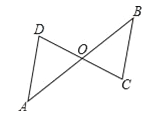
【题目】如图,点O是线段AB和线段CD的中点.
(1)求证:△AOD≌△BOC;
(2)求证:AD∥BC.
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 过直线外一点可以画无数条直线与这条直线垂直
B. 过直线外一定点不可以画这条直线的垂线
C. 过直线外一点可以画这条直线的一条垂线
D. 如果两条直线不相交,那么这两条直线有可能互相垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】潼南绿色无公害蔬菜基地有甲、乙两种植户,他们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
种植户 | 种植A类蔬菜面积 | 种植B类蔬菜面积 | 总收入 |
甲 | 3 | 1 | 12500 |
乙 | 2 | 3 | 16500 |
说明:不同种植户种植的同类蔬菜每亩平均收入相等.
(1)求A、B两类蔬菜每亩平均收入各是多少元?
(2)某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有租地方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在ABCD中,E,F是对角线BD上的两点,则以下条件不能判断四边形AECF为平行四边形的是( ) 
A.BE=DF
B.AF⊥BD,CE⊥BD
C.∠BAE=∠DCF
D.AF=CE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AC的中点,N是BC的中点,则线段MN的长度是( )
A.7cm
B.3cm
C.7cm或3cm
D.5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
“共享单车”是指企业与政府合作,在校园、地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车共享的一种服务,是共享经济的一种新形态.共享单车的出现让更多的用户有了更好的代步选择.自行车也代替了一部分公共交通甚至打车的出行.
Quest Mobile监测的M型与O型单车从2016年10月——2017年1月的月度用户使用情况如下表所示:
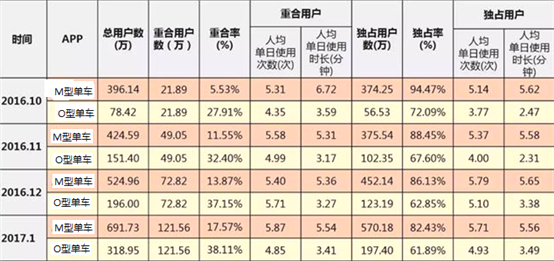
根据以上材料解答下列问题:
(1)仔细阅读上表,将O型单车总用户数用折线图表示出来,并在图中标明相应数据;
(2)根据图表所提提供的数据,选择你所感兴趣的方面,写出一条你发现的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥DE,AB=DE,BF=EC.
(1)求证:AC∥DF;
(2)若CF=1个单位长度,能由△ABC经过图形变换得到△DEF吗?若能,请你用轴对称、平移或旋转等描述你的图形变换过程;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题(保留作图痕迹,不写画法).
(1)请在坐标系中,画出△ABC关于y轴对称的△A′B′C′. 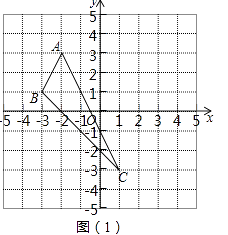
(2)如图(2),A与B是两个居住社区,OC与OD是两条交汇的公路,欲建立一个超市M,使它到A、B两个社区的距离相等,且到两条公路OC、OD的距离也相等.请利用尺规作图,确定超市M的位置. 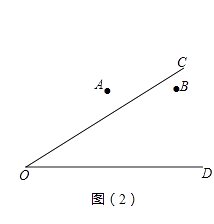
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com