
【题目】已知点A(1,a),将线段OA平移至线段BC,B(b,0),a是m+6n的算术平方根,![]() =3,n=
=3,n=![]() ,且m<n,正数b满足(b+1)2=16.
,且m<n,正数b满足(b+1)2=16.
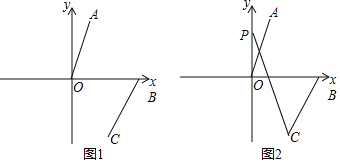
(1)直接写出A、B两点坐标为:A ,B ;
(2)如图1,连接AB、OC,求四边形AOCB的面积;
(3)如图2,若∠AOB=a,点P为y轴正半轴上一动点,试探究∠CPO与∠BCP之间的数量关系.
【答案】(1)A(1,3); B(3,0);(2)S四边形AOCB=9;(3)∠BCP﹣∠CPO=90°﹣a.
【解析】
(1)根据算术平方根、二次根式和偶次幂解答即可;
(2)根据平移的性质和三角形的面积解答即可;
(3)过点P作PD∥OA,可证得PD∥OA∥BC,由平行线的性质进行解答即可.
(1)∵a是m+6n的算术平方根,![]() =3,n=
=3,n=![]() ,且m<n,正数b满足(b+1)2=16.
,且m<n,正数b满足(b+1)2=16.
∴m=﹣3,n=2,a=3,b=3,
∴A(1,3),B(3,0);
故答案为:A(1,3); B(3,0);
(2)如图1所示:
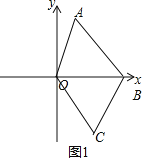
由题意知:C(2,﹣3),
∵B(3,0),
∴OB=3,
∴S四边形AOCB=S△AOB+S△BOC=![]() ,
,
故答案为:9;
(3)过点P作PD∥OA,如图2所示:

∵OA∥BC,
∴PD∥OA∥BC
∴∠BCP=∠DPC,∠DPO=∠AOP.
∵∠AOB=a,
∴∠AOP=90°﹣∠AOB=90°﹣a.
∴∠DPO=90°﹣a.
∵∠DPC=∠DPO+∠CPO,
∴∠BCP=∠CPO+90°﹣a,
即∠BCP﹣∠CPO=90°﹣a,
故答案为:∠BCP﹣∠CPO=90°﹣a.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,点D是BC上一点,将△ABD沿AD翻折后得到△AED,边AE交射线BC于点F.(友情提醒:翻折前后的两个三角形的对应边相等,对应角相等.)



(1)如图①,当AE⊥BC时,求证:DE∥AC.
(2)若![]() ,∠BAD=x° .
,∠BAD=x° .
①如图②,当DE⊥BC时,求x的值;
②是否存在这样的x的值,使得△DEF中有两个角相等.若存在,并求x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点C顺时针旋转m°得到△EDC,若点A、D、E在同一直线上,∠ACB=n°,则∠ADC的度数是( )

A. (m﹣n)°B. (90+n-![]() m)°C. (90-
m)°C. (90-![]() n+m)°D. (180﹣2n﹣m)°
n+m)°D. (180﹣2n﹣m)°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣ ![]() x+m(m>0)的图象与x轴、y轴分别交于点A,B,点C在线段OA上,点C的横坐标为n,点D在线段AB上,且AD=2BD,将△ACD绕点D旋转180°后得到△A1C1D.
x+m(m>0)的图象与x轴、y轴分别交于点A,B,点C在线段OA上,点C的横坐标为n,点D在线段AB上,且AD=2BD,将△ACD绕点D旋转180°后得到△A1C1D.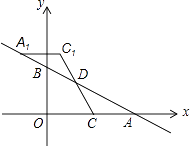
(1)若点C1恰好落在y轴上,试求 ![]() 的值;
的值;
(2)当n=4时,若△A1C1D被y轴分得两部分图形的面积比为3:5,求该一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
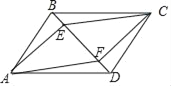
【题目】如图,在ABCD中,经过A,C两点分别作AE⊥BD,CF⊥BD,E,F为垂足.
(1)求证:△AED≌△CFB;
(2)求证:四边形AFCE是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
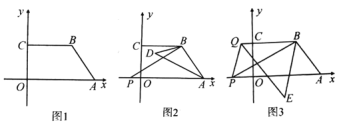
【题目】在平面直角坐标系中,四边形 OABC 的顶点 A、C 分别在 x 轴和 y 轴上,顶点B 在第一象限,OA//CB.
(1)如图 1,若点 A(6,0),B(4,3),点 M 是 y 轴上一点,且 SBCM SAOM ,求点 M的坐标;
(2)如图 2,点 P 是 x 轴上点 A 左边的一点,连接 PB,∠PBC 和∠PAB 的角平分线交于点D,求证:∠ABP+2∠ADB=180°;
(3)如图 3,点 P 是 x 轴上点 A 左边的一点,点 Q 是射线 BC 上一点,连接 PB、PQ,∠ABP和∠BQP 的平分线相交于点 E,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AD是BC边上的中线,过点D作BA的平行线交AC于点O,过点A作BC的平行线交DO的延长线于点E,连接CE.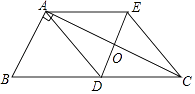
(1)求证:四边形ADCE是菱形;
(2)作出△ABC外接圆,不写作法,请指出圆心与半径;
(3)若AO:BD= ![]() :2,求证:点E在△ABC的外接圆上.
:2,求证:点E在△ABC的外接圆上.
查看答案和解析>>
科目:初中数学 来源: 题型:
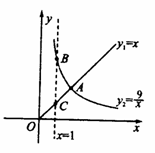
【题目】函数 yl= x ( x ≥0 ) , ![]() ( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3
( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3 ![]() 时, ③ 当 x =1时, BC = 8
时, ③ 当 x =1时, BC = 8
④ 当 x 逐渐增大时, yl 随着 x 的增大而增大,y2随着 x 的增大而减小.其中正确结论的序号是_ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是边长为1的正方形ABCD的边AB上任意一点(不含A,B),过B,C,E三点的圆与BD相交于点F,与CD相交于点G,与∠ABC的外角平分线相交于点H.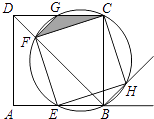
(1)求证:四边形EFCH是正方形;
(2)设BE=x,△CFG的面积为y,求y与x的函数关系式,并求y的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com