
����Ŀ��ѧУ���ھٰ���һ��һ�ȵľ����ж�������ij�༶���Ŀ��Ҫ���빺��A��B���ֵ��ߣ���֪����1��A���߱ȹ���1��B���߶�10Ԫ������2��A���ߺ�3��B���߹���Ҫ45Ԫ��
��1������һ��A���ߺ�һ��B���߸���Ҫ����Ԫ��
��2�����ݰ༶�������Ҫ�����ֵ��߹�60�����ҹ������ֵ��ߵ��ܷ��ò�����620Ԫ��
�����ʵ���A������ټ���
��������A���߹���ļ���������B���߹���������ð༶���м��ַ�������д�����з�������������ٷ���Ϊ����Ԫ��
���𰸡���1������һ��A������Ҫ15Ԫ������һ��B������Ҫ5Ԫ;��2����A��������32�������ð༶����3�ֹ���������1��A���߹���30����B���߹���30��������2��A���߹���31����B���߹���29��������3��A���߹���32����B���߹���28�������ٹ������Ϊ600Ԫ��
��������
��1���蹺��һ��A������ҪxԪ������һ��B������ҪyԪ������������1��A���߱ȹ���1��B���߶�10Ԫ������2��A���ߺ�3��B���߹���Ҫ45Ԫ�������ɵó�����x��y�Ķ�Ԫһ�η����飬��֮���ɵó����ۣ�
��2���蹺��A����m��������B���ߣ�60-m�������ٸ����ܼ�=������������Ϲ������ֵ��ߵ��ܷ��ò�����620Ԫ�����ɵó�����m��һԪһ�β���ʽ����֮ȡ���е��������ֵ���ɵó����ۣ�����A���߹���ļ���������B���߹�����������ɵó�����m��һԪһ�β���ʽ����֮���ɵó�m��ȡֵ��Χ����ϢٵĽ��ۼ�mΪ����ֵ���ɵó��������������������������ã��ȽϺɵó����ٷ��ã�
��1���蹺��һ��A������ҪxԪ������һ��B������ҪyԪ��
�����⣬�ã�![]() ��
��
��ã�![]() ��
��
�𣺹���һ��A������Ҫ15Ԫ������һ��B������Ҫ5Ԫ��
��2���蹺��A����m��������B���ߣ�60��m������
�������⣬�ã�15m+5��60��m����620��
��ã�m��32��
��A��������32����
�������⣬�ã�m��60��m��
��ã�m��30��
����m��32����m������
��m��30��31��32��
���ð༶����3�ֹ���������1��A���߹���30����B���߹���30��������2��A���߹���31����B���߹���29��������3��A���߹���32����B���߹���28����
����1�������15��30+5��30��600��Ԫ����
����2�������15��31+5��29��610��Ԫ����
����3�������15��32��5��28��620��Ԫ����
��600��610��620��
�����ٹ������Ϊ600Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ֶ��������y��dm�������ȳ�x��dm����һ�κ�������������ȳ�Ϊ6dmʱ������Ϊ45.5dm����������ȳ�Ϊ14dmʱ������Ϊ105.5dm��
��1��д��y��x֮��Ĺ�ϵʽ��
��2�����ö����ȳ�10dmʱ��������Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ĸ��ֻ�Ӧ��ͼ���У�������Գ�ͼ���������ĶԳ�ͼ�ε��ǣ� ��
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У���A��2��0������B��0��1��������A��ֱ��l��ֱ���߶�AB����P��ֱ��l��һ���㣬����P��PC��x�ᣬ����ΪC���ѡ�ACP��AP����180�㣬ʹ��C���ڵ�D��������A��D��PΪ��������������ABP���ƣ�����������������ĵ�P������Ϊ �� 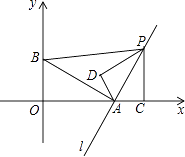
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֽƬABCD�У�AB��8����ֽƬ�۵���ʹ����B���ڱ�AD�ϵ�E�㴦���ۺ۵�һ��G���ڱ�BC�ϣ�
(1)��ͼ1�����ۺ۵���һ��F��AB������AE��4ʱ����AF�ij�
(2)��ͼ2�����ۺ۵���һ��F��AD������BG��10ʱ��
����֤��EF��EG������AF�ij���
(3)��ͼ3�����ۺ۵���һ��F��AD���ϣ�B��Ķ�Ӧ��E�ڳ������ڲ���E��AD�ľ���Ϊ2cm����BG��10ʱ����AF�ij���
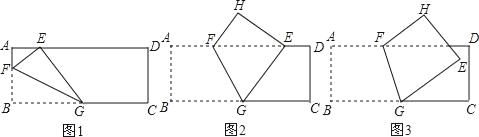
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��![]() ��
��![]() ���Ա߷ֱ���
���Ա߷ֱ���![]() ����
����![]() ��������
��������![]() �����
�����![]() Ϊ���������Σ�����ȱ������ξ�������������.
Ϊ���������Σ�����ȱ������ξ�������������.
��1����![]() ���ж�
���ж�![]() �Ƿ�Ϊ���������Σ���˵�����ɣ�
�Ƿ�Ϊ���������Σ���˵�����ɣ�
��2����![]() ��
��![]() ����
����![]() �ij���
�ij���
��3����ͼ2��������������![]() �У�
��![]() ����
����![]() ��
��![]() ���ϵ��е㣬����
���ϵ��е㣬����![]() ��
��![]() ��
��![]() �ָ��2�������Σ�����
�ָ��2�������Σ�����![]() �����������Σ�
������������![]() ����
����![]() Ϊ�ĵ��������Σ���
Ϊ�ĵ��������Σ���![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABC��������ABC����8��8�����У�λ����ͼ��ʾ��A����3��1����B����2��4����

��1�������ڷ����н���ֱ������ϵ����д��C������ꣻ
��2���ѡ�ABC����ƽ��1����λ���ȣ�������ƽ��2����λ���ȣ����㻭��ƽ�ƺ�ġ�A1B1C1������ABC�ڲ�һ��P������Ϊ��a��b�������P�Ķ�Ӧ��P1�������� ��
��3����x���ϴ���һ��D��ʹ��DB1C1���������3�������������ĵ�D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=3��AE��BD������ΪE��ED=3BE����P��Q�ֱ���BD��AD�ϣ���AP+PQ��СֵΪ �� 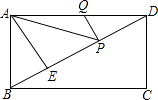
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ABCD�Ƶ�A��ʱ����ת30�㣬�õ�
ABCD�Ƶ�A��ʱ����ת30�㣬�õ�![]() AB��C��D�䣬����B�����B�Ƕ�Ӧ�㣬����B��ǡ������BC���ϣ����C=�� ��
AB��C��D�䣬����B�����B�Ƕ�Ӧ�㣬����B��ǡ������BC���ϣ����C=�� ��
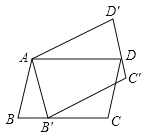
A. 105��B. 120��C. 135��D. 150��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com