
【题目】如图,在直角坐标系中,点A(2,0),点B(0,1),过点A的直线l垂直于线段AB,点P是直线l上一动点,过点P作PC⊥x轴,垂足为C,把△ACP沿AP翻折180°,使点C落在点D处.若以A,D,P为顶点的三角形与△ABP相似,则所有满足此条件的点P的坐标为 . 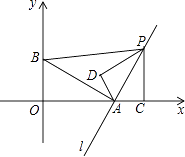
【答案】P(4,4),p(0,﹣4),P( ![]() ,﹣1),P(
,﹣1),P( ![]() ,1)
,1)
【解析】解:∵点A(2,0),点B(0,1),
∴直线AB的解析式为y=﹣ ![]() x+1
x+1
∵直线l过点A(2,0),且l⊥AB,
∴直线L的解析式为;y=2x﹣4,
∠BAO+∠PAC=90°,
∵PC⊥x轴,
∴∠PAC+∠APC=90°,
∴∠BAO=∠APC,
∵∠AOB=∠ACP,
∴△AOB∽△PCA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
设AC=m,则PC=2m,
∵△PCA≌△PDA,
∴AC=AD,PC=PD,
∴ ![]() =
= ![]() =
= ![]() ,
,
如图1:当△PAD∽△PBA时,
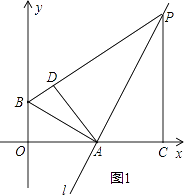
则 ![]() =
= ![]() ,
,
则 ![]() =
= ![]() =
= ![]() ,
,
∵AB= ![]() =
= ![]() ,
,
∴AP=2 ![]() ,
,
∴m2+(2m)2=(2 ![]() )2,
)2,
∴m=±2,
当m=2时,PC=4,OC=4,P点的坐标为(4,4),
当m=﹣2时,如图2,

PC=4,OC=0,P点的坐标为(0,﹣4),
如图3,若△PAD∽△BPA,
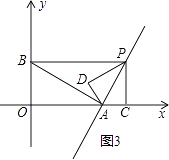
则 ![]() =
= ![]() =
= ![]() ,
,
PA= ![]() AB=
AB= ![]() ,
,
则m2+(2m)2=( ![]() )2,
)2,
∴m=± ![]() ,
,
当m= ![]() 时,PC=1,OC=
时,PC=1,OC= ![]() ,P点的坐标为(
,P点的坐标为( ![]() ,1),
,1),
当m=﹣ ![]() 时,如图4,PC=1,OC=
时,如图4,PC=1,OC= ![]() ,P点的坐标为(
,P点的坐标为( ![]() ,﹣1);
,﹣1);
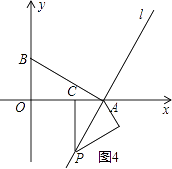
所以答案是:P(4,4),p(0,﹣4),P( ![]() ,﹣1),P(
,﹣1),P( ![]() ,1).
,1).
【考点精析】关于本题考查的勾股定理的概念和翻折变换(折叠问题),需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④BA+BC=2BF,其中正确的结论有________(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道对于一个图形,通过不同的方法计算图形的面积时,可以得到一个数学等式.例如由图1可以得到![]() .请回答下列问题:
.请回答下列问题:

(1)写出图2中所表示的数学等式是 ;
(2)如图3,用四块完全相同的长方形拼成正方形,用不同的方法,计算图中阴影部分的面积,你能发现什么?(用含有![]() ,
,![]() 的式子表示) ;
的式子表示) ;
(3)通过上述的等量关系,我们可知: 当两个正数的和一定时,它们的差的绝对值越小,则积越 (填“ 大”“或“小”);当两个正数的积一定时,它们的差的绝对值越小,则和越 (填“ 大”或“小”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD的对角线交于点E,且AE=EC,BE=ED,以AB为直径的半圆过点E,圆心为O.
(1)利用图1,求证:四边形ABCD是菱形.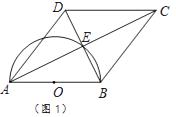
(2)如图2,若CD的延长线与半圆相切于点F,且直径AB=8.
①△ABD的面积为 .
② ![]() 的长 .
的长 . 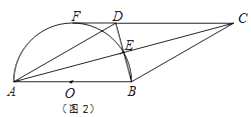
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校近期举办了一年一度的经典诵读比赛.某班级因节目需要,须购买A、B两种道具.已知购买1件A道具比购买1件B道具多10元,购买2件A道具和3件B道具共需要45元.
(1)购买一件A道具和一件B道具各需要多少元?
(2)根据班级情况,需要这两种道具共60件,且购买两种道具的总费用不超过620元.
①请问道具A最多购买多少件?
②若其中A道具购买的件数不少于B道具购买件数,该班级共有几种方案?试写出所有方案,并求出最少费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小华用黑白棋子组成的一组图案,第1个图案由1个黑子组成,第2个图案由1个黑子和6个白子组成,第3个图案由13个黑子和6个白子组成,按照这样的规律排列下去,则第8个图案中共有( )个棋子.

A.159B.169C.172D.132
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,要使四边形ABCD为平行四边形,则应添加的条件是______.(添加一个条件即可,不添加其它的点和线).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com