
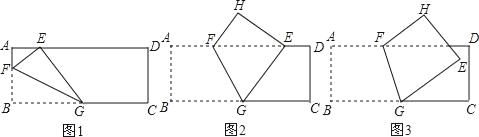
【题目】如图,长方形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD上的E点处,折痕的一端G点在边BC上.
(1)如图1,当折痕的另一端F在AB边上且AE=4时,求AF的长
(2)如图2,当折痕的另一端F在AD边上且BG=10时,
①求证:EF=EG.②求AF的长.
(3)如图3,当折痕的另一端F在AD边上,B点的对应点E在长方形内部,E到AD的距离为2cm,且BG=10时,求AF的长.
【答案】(1)AF=3;(2)①证明见解析;②AF=6;(3)AF=![]() .
.
【解析】
(1)根据翻折的性质可得BF=EF,然后用AF表示出EF,在Rt△AEF中,利用勾股定理列出方程求解即可;
(2)①根据翻折的性质可得∠BGF=∠EGF,再根据两直线平行,内错角相等可得∠BGF=∠EFG,从而得到∠EGF=∠EFG,再根据等角对等边证明即可;
②根据翻折的性质可得EG=BG,HE=AB,FH=AF,然后在Rt△EFH中,利用勾股定理列式计算即可得解;
(3)设EH与AD相交于点K,过点E作MN∥CD分别交AD、BC于M、N,然后求出EM、EN,在Rt△ENG中,利用勾股定理列式求出GN,再根据△GEN和△EKM相似,利用相似三角形对应边成比例列式求出EK、KM,再求出KH,然后根据△FKH和△EKM相似,利用相似三角形对应边成比例列式求解即可.
(1)∵纸片折叠后顶点B落在边AD上的E点处,
∴BF=EF,
∵AB=8,∴EF=8﹣AF,
在Rt△AEF中,AE2+AF2=EF2,
即42+AF2=(8﹣AF)2,
解得AF=3;
(2)①∵纸片折叠后顶点B落在边AD上的E点处,
∴∠BGF=∠EGF,
∵长方形纸片ABCD的边AD∥BC,
∴∠BGF=∠EFG,
∴∠EGF=∠EFG,
∴EF=EG;
②∵纸片折叠后顶点B落在边AD上的E点处,
∴EG=BG=10,HE=AB=8,FH=AF,
∴EF=EG=10,
在Rt△EFH中,FH=![]() =
=![]() =6,
=6,
∴AF=FH=6;
(3)如图3,设EH与AD相交于点K,过点E作MN∥CD分别交AD、BC于M、N,
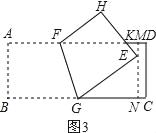
∵E到AD的距离为2cm,
∴EM=2,EN=8﹣2=6,
在Rt△ENG中,GN=![]() =
=![]() =8,
=8,
∵∠GEN+∠KEM=180°﹣∠GEH=180°﹣90°=90°,
∵∠GEN+∠NGE=180°﹣90°=90°,
∴∠KEM=∠NGE,
又∵∠ENG=∠KME=90°,
∴△GEN∽△EKM,
∴![]() ,
,
即![]() ,
,
解得EK=![]() ,KM=
,KM=![]() ,
,
∴KH=EH﹣EK=8﹣![]() =
=![]() ,
,
∵∠FKH=∠EKM,∠H=∠EMK=90°,
∴△FKH∽△EKM,
∴![]() ,
,
即 ,
,
解得FH=![]() ,
,
∴AF=FH=![]() .
.


科目:初中数学 来源: 题型:
【题目】网络商店(简称网店)是近年来迅速兴起的一种电子商务形式,小明的网店销售红枣、小米两种商品的相关信息如下表:
商品 | 红枣 | 小米 |
规格 | 1kg/袋 | 2kg/袋 |
成本(元/袋) | 40 | 38 |
售价(元/袋) | 60 | 54 |
根据上表提供的信息,解答下列问题
(1)已知今年前四个月,小明的网店销售上表中规格的红枣和小米共2000kg,获得利润2.8万元,求这前四个月小明的网店销售这种规格的红枣和小米各多少袋?
(2)根据之前的销售情况,估计今年5月到12月这后八个月,小明的网店还能销售同规格的红枣和小米共4000kg,其中,红枣的销售量不低于1200kg.假设这后八个月,销售红枣x(kg),销售红枣和小米获得的总利润为y(元),求出y与x之间的函数关系式,并求出这后八个月,小明的网店销售这种规格的红枣和小米至少获得总利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道对于一个图形,通过不同的方法计算图形的面积时,可以得到一个数学等式.例如由图1可以得到![]() .请回答下列问题:
.请回答下列问题:

(1)写出图2中所表示的数学等式是 ;
(2)如图3,用四块完全相同的长方形拼成正方形,用不同的方法,计算图中阴影部分的面积,你能发现什么?(用含有![]() ,
,![]() 的式子表示) ;
的式子表示) ;
(3)通过上述的等量关系,我们可知: 当两个正数的和一定时,它们的差的绝对值越小,则积越 (填“ 大”“或“小”);当两个正数的积一定时,它们的差的绝对值越小,则和越 (填“ 大”或“小”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划在某商店购买秋季运动会的奖品,若买5个篮球和10个足球需花费1150元,若买9个篮球和6个足球需花费1170元.
(1)篮球和足球的单价各是多少元?
(2)实际购买时,正逢该商店进行促销.所有体育用品都按原价的八折优惠出售,学校购买了若干个篮球和足球,恰好花费1760元.请直接写出学校购买篮球和足球的个数各是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校近期举办了一年一度的经典诵读比赛.某班级因节目需要,须购买A、B两种道具.已知购买1件A道具比购买1件B道具多10元,购买2件A道具和3件B道具共需要45元.
(1)购买一件A道具和一件B道具各需要多少元?
(2)根据班级情况,需要这两种道具共60件,且购买两种道具的总费用不超过620元.
①请问道具A最多购买多少件?
②若其中A道具购买的件数不少于B道具购买件数,该班级共有几种方案?试写出所有方案,并求出最少费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:如图1,在△ABC中,∠C=90°,分别以AC、BC为边向外侧作正方形ACDE和正方形BCFG.
(1)△ABC与△DCF面积的关系是;(请在横线上填写“相等”或“不相等”)
(2)拓展探究:若∠C≠90°,(1)中的结论还成立吗?若成立,请结合图2给出证明;若不成立,请说明理由;
(3)解决问题:如图3,在四边形ABCD中,AC⊥BD,且AC与BD的和为10,分别以四边形ABCD的四条边为边向外侧作正方形ABFE、正方形BCHG、正方形CDJI、正方形DALK,运用(2)的结论,图中阴影部分的面积和是否有最大值?如果有,请求出最大值,如果没有,请说明理由.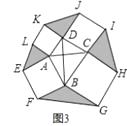
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:在综合与实践课上,同学们以“已知三角形三边的长度,求三角形面积”为主题开展数学活动,小颖想到借助正方形网格解决问题.图1,图2都是8×8的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点.

操作发现:小颖在图1中画出△ABC,其顶点A,B,C都是格点,同时构造正方形BDEF,使它的顶点都在格点上,且它的边DE,EF分别经过点C,A,她借助此图求出了△ABC的面积.
(1)在图1中,小颖所画的△ABC的三边长分别是AB=__________,BC=__________,AC=__________;△ABC的面积为__________.
解决问题:(2)已知△ABC中,AB=![]() ,BC=2
,BC=2![]() ,AC=5
,AC=5![]() ,请你根据小颖的思路,在图2的正方形网格中画出△ABC,并计算△ABC的面积.
,请你根据小颖的思路,在图2的正方形网格中画出△ABC,并计算△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com