
【题目】问题情境:在综合与实践课上,同学们以“已知三角形三边的长度,求三角形面积”为主题开展数学活动,小颖想到借助正方形网格解决问题.图1,图2都是8×8的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点.

操作发现:小颖在图1中画出△ABC,其顶点A,B,C都是格点,同时构造正方形BDEF,使它的顶点都在格点上,且它的边DE,EF分别经过点C,A,她借助此图求出了△ABC的面积.
(1)在图1中,小颖所画的△ABC的三边长分别是AB=__________,BC=__________,AC=__________;△ABC的面积为__________.
解决问题:(2)已知△ABC中,AB=![]() ,BC=2
,BC=2![]() ,AC=5
,AC=5![]() ,请你根据小颖的思路,在图2的正方形网格中画出△ABC,并计算△ABC的面积.
,请你根据小颖的思路,在图2的正方形网格中画出△ABC,并计算△ABC的面积.
科目:初中数学 来源: 题型:
【题目】某中学为了绿化校园,计划购买一批榕树和香樟树,经市场调查,榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.
(1)榕树和香樟树的单价各是多少?
(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵数不少于榕树的1.5倍,请你算算该校本次购买榕树和香樟树共有哪几种方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
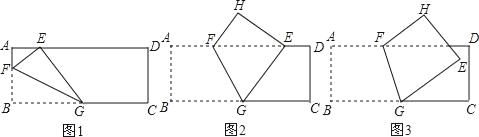
【题目】如图,长方形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD上的E点处,折痕的一端G点在边BC上.
(1)如图1,当折痕的另一端F在AB边上且AE=4时,求AF的长
(2)如图2,当折痕的另一端F在AD边上且BG=10时,
①求证:EF=EG.②求AF的长.
(3)如图3,当折痕的另一端F在AD边上,B点的对应点E在长方形内部,E到AD的距离为2cm,且BG=10时,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形ABC(记作△ABC)在8×8方格中,位置如图所示,A(-3,1),B(-2,4).

(1)请你在方格中建立直角坐标系,并写出C点的坐标;
(2)把△ABC向下平移1个单位长度,再向右平移2个单位长度,请你画出平移后的△A1B1C1,若△ABC内部一点P的坐标为(a,b),则点P的对应点P1的坐标是 .
(3)在x轴上存在一点D,使△DB1C1的面积等于3,求满足条件的点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上行驶速度不得超过70 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30 m处,过了2 s后,测得小汽车与车速检测仪间距离为50 m,这辆小汽车超速了吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,过点C作CE⊥DB交DB的延长线于点E,直线AB与CE相交于点F.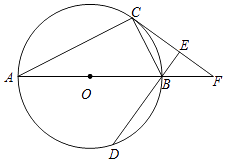
(1)求证:CF为⊙O的切线;
(2)填空:当∠CAB的度数为时,四边形ACFD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线MN与直线PQ相交于O,∠POM=60°,点A在射线OP上运动,点B在射线OM上运动.

(1)如图1,∠BAO=70°,已知AE、BE分别是∠BAO和∠ABO角的平分线,试求出∠AEB的度数.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)在(2)的条件下,在△CDE中,如果有一个角是另一个角的2倍,请直接写出∠DCE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com