
【题目】实数a,b在数轴上对应点的位置如图所示,化简|a|+ ![]() 的结果是( )
的结果是( )![]()
A.﹣2a+b
B.2a﹣b
C.﹣b
D.b
科目:初中数学 来源: 题型:
【题目】我们知道对于一个图形,通过不同的方法计算图形的面积时,可以得到一个数学等式.例如由图1可以得到![]() .请回答下列问题:
.请回答下列问题:

(1)写出图2中所表示的数学等式是 ;
(2)如图3,用四块完全相同的长方形拼成正方形,用不同的方法,计算图中阴影部分的面积,你能发现什么?(用含有![]() ,
,![]() 的式子表示) ;
的式子表示) ;
(3)通过上述的等量关系,我们可知: 当两个正数的和一定时,它们的差的绝对值越小,则积越 (填“ 大”“或“小”);当两个正数的积一定时,它们的差的绝对值越小,则和越 (填“ 大”或“小”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:在综合与实践课上,同学们以“已知三角形三边的长度,求三角形面积”为主题开展数学活动,小颖想到借助正方形网格解决问题.图1,图2都是8×8的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点.

操作发现:小颖在图1中画出△ABC,其顶点A,B,C都是格点,同时构造正方形BDEF,使它的顶点都在格点上,且它的边DE,EF分别经过点C,A,她借助此图求出了△ABC的面积.
(1)在图1中,小颖所画的△ABC的三边长分别是AB=__________,BC=__________,AC=__________;△ABC的面积为__________.
解决问题:(2)已知△ABC中,AB=![]() ,BC=2
,BC=2![]() ,AC=5
,AC=5![]() ,请你根据小颖的思路,在图2的正方形网格中画出△ABC,并计算△ABC的面积.
,请你根据小颖的思路,在图2的正方形网格中画出△ABC,并计算△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y1=kx+b的图象分别交x轴,y轴于A、B两点,与反比例函数y2= ![]() 的图象交于C、D两点,已知点C的坐标为(﹣4,﹣1),点D的横坐标为2.
的图象交于C、D两点,已知点C的坐标为(﹣4,﹣1),点D的横坐标为2.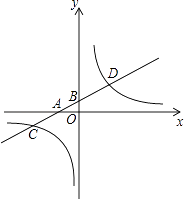
(1)求反比例函数与一次函数的解析式;
(2)直接写出当x为何值时,y1>y2?
(3)点P是反比例函数在第一象限的图象上的点,且点P的横坐标大于2,过点P做x轴的垂线,垂足为点E,当△APE的面积为3时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)尺规作图:如图1,请在x轴上作出表示(![]() ,0)的点(保留清晰作图痕迹,不写作法).
,0)的点(保留清晰作图痕迹,不写作法).
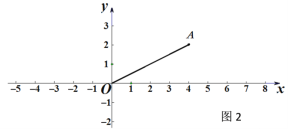
(2)如图2,已知点A(4,2),点B在x轴上,若∠OAB=90°,试求点B的坐标;
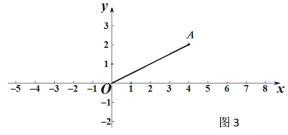
(3)如图3,已知点A(4,2),点C在x轴上,若△OAC为等腰三角形,试求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,要使四边形ABCD为平行四边形,则应添加的条件是______.(添加一个条件即可,不添加其它的点和线).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明坐在堤边A处垂钓,河堤AC与水平面的夹角为30°,AC的长为 ![]() 米,钓竿AO与水平线的夹角为60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
米,钓竿AO与水平线的夹角为60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.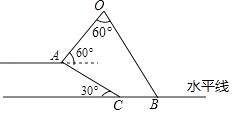
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校数学兴趣小组为测得大厦AB的高度,在大厦前的平地上选择一点C,测得大厦顶端A的仰角为30°,再向大厦方向前进80米,到达点D处(C,D,B三点在同一直线上),又测得大厦顶端A的仰角为45°,请你计算该大厦的高度.(精确到0.1米,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)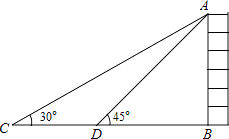
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com