
【题目】(1)尺规作图:如图1,请在x轴上作出表示(![]() ,0)的点(保留清晰作图痕迹,不写作法).
,0)的点(保留清晰作图痕迹,不写作法).
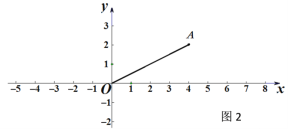
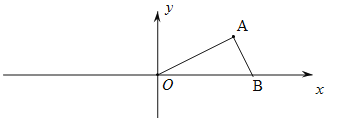
(2)如图2,已知点A(4,2),点B在x轴上,若∠OAB=90°,试求点B的坐标;
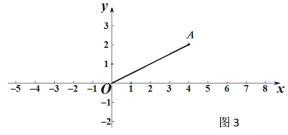
(3)如图3,已知点A(4,2),点C在x轴上,若△OAC为等腰三角形,试求点C的坐标.
【答案】(1)答案见解析;(2)(5,0);(3)(8,0),(2.5,0),(![]() ,0),(-
,0),(-![]() ,0).
,0).
【解析】
(1)过2作y轴的垂线,过-4作x轴的垂线,交于点B,连接OB,以O为圆心,OB为半径作弧交x轴负半轴于点A,则点A就是所求的点.
(2)用待定系数法求出直线OA的解析式.设直线AB为y=ax+b,由BA⊥OA,得到a=-2,把A(4,2)代入得到b的值,从而得到直线AB的解析式,令y=0,求得x的值,即可得到结论.
(3)分三种情况讨论:①以O为圆心,OA为半径作圆O交x轴于点C1,C2;②以A为圆心,OA为半径作圆A交x轴于点O,C3;③作OA的垂直平分线交x轴于点C4.分别求出点C的坐标即可.
(1)如图,过2作y轴的垂线,过-4作x轴的垂线,交于点B,连接OB,以O为圆心,OB为半径作弧交x轴负半轴于点A,则OA=OB=![]() ,∴A(
,∴A(![]() ,0).
,0).
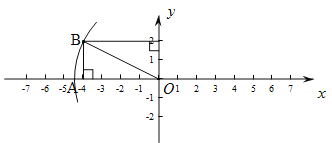
(2)设直线OA为y=kx,把A(4,2)代入得:2=4k,解得:k=![]() ,∴直线OA的解析式为y=
,∴直线OA的解析式为y=![]() x.设直线AB为y=ax+b.
x.设直线AB为y=ax+b.
∵BA⊥OA,则a=-2,∴直线AB为y=-2x+b,把A(4,2)代入得:2=-2×4+b,解得:b=10,∴y=-2x+10.在y=-2x+10中,令y=0,解得:x=5,∴B(5,0).
(3)分三种情况讨论:
①以O为圆心,OA为半径作圆O交x轴于点C1,C2,则OC1=OC2=OA=![]() ,∴C1(
,∴C1(![]() ,0),C2(
,0),C2(![]() ,0);
,0);
②以A为圆心,OA为半径作圆A交x轴于点O,C3,则OC3=2×4=8,∴C3(8,0);
③作OA的垂直平分线交x轴于点C4,则OC4=AC4.设C4(x,0),则![]() ,解得:x=2.5,∴C4(2.5,0).
,解得:x=2.5,∴C4(2.5,0).
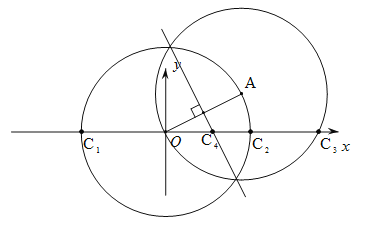
综上所述:点C的坐标为(8,0)或(2.5,0)或(![]() ,0)或(-
,0)或(-![]() ,0).
,0).


科目:初中数学 来源: 题型:
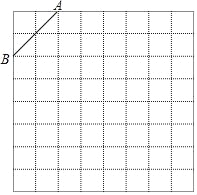
【题目】如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
(1)在网格中建立平面直角坐标系,使A点坐标为(﹣2,4),B点坐标为(﹣4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是 ;
(3)求△ABC中BC边上的高长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上行驶速度不得超过70 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30 m处,过了2 s后,测得小汽车与车速检测仪间距离为50 m,这辆小汽车超速了吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,过点C作CE⊥DB交DB的延长线于点E,直线AB与CE相交于点F.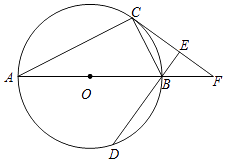
(1)求证:CF为⊙O的切线;
(2)填空:当∠CAB的度数为时,四边形ACFD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市决定购买A、B两种树苗对某段道路进行绿化改造,已知购买A种树苗9棵,B种树苗4棵,需要700元;购买A种树苗3棵,B种树苗5棵,则需要380元.
(1)求购买A、B两种树苗每颗各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗不能少于60棵,且用于购买这两种树苗的资金不能超过5260元.若购进这两种树苗共100棵,则有哪几种购买方案?哪种方案最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系xOy中的位置如图所示.

(1)作△ABC关于点C成中心对称的△A1B1C1.
(2)将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2.
(3)在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王教授和他的孙子小强星期天一起去爬山,来到山脚下,小强让爷爷先上山,然后追赶爷爷,如图所示,两条线段分别表示小强和爷爷离开山脚的距离y(米)与爬山所用时间x(分钟)的关系(小强开始爬山时开始计时),请看图回答下列问题:
(1)爷爷比小强先上了多少米?山顶离山脚多少米?
(2)谁先爬上山顶?小强爬上山顶用了多少分钟?
(3)图中两条线段的交点表示什么意思?这时小强爬山用时多少?离山脚多少米?
(4)直角坐标系中的横轴和纵轴上的单位长度取得不一致,这对问题的结论有影响吗?允许这样做吗?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com