
【题目】如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
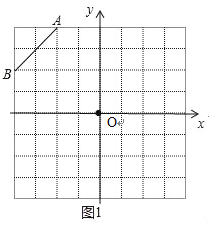
(1)在网格中建立平面直角坐标系,使A点坐标为(﹣2,4),B点坐标为(﹣4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是 ;
(3)求△ABC中BC边上的高长.
【答案】(1)见解析;(2)(﹣1,1);(3)![]() .
.
【解析】
(1)根据A点坐标向右两个单位,再向下4个单位,可得原点,建立直角坐标系;
(2)根据勾股定理和等腰三角形的判定,可得点C的坐标,
(3)根据勾股定理,求出BC,根据图形割补法,可得面积,再根据三角形的面积公式即可得到结论.
(1)如图1:
(2)如图2:
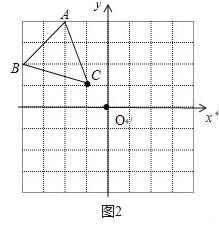
在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是 (﹣1,1);
故答案为:(﹣1,1);
(3) 根据勾股定理得:BC=![]() ,
,
∵S△ABC=3×3﹣![]() ×1×3﹣
×1×3﹣![]() ×1×3﹣
×1×3﹣![]() ×2×2=4=
×2×2=4=![]() BC×BC边上的高 ,
BC×BC边上的高 ,
∴△ABC中BC边上的高=![]() =
=![]() .
.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】已知坐标平面内的三个点A(1,3),B(3,1),O(0,0),把△ABO向下平移3个单位再向右平2个单位后得△DEF.

(1)直接写出A、B、O三个对应点D、E、F的坐标;
(2)求△DEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BE平分∠ABC交AD于点E,F为BE上一点,连接DF,过F作FG⊥DF交BC于点G,连接BD交FG于点H,若FD=FG,BF=3 ![]() ,BG=4,则GH的长为 .
,BG=4,则GH的长为 . 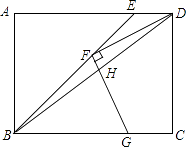
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,长方形ABCD的顶点B、C分别在边OM、ON上,当B在边OM上运动时,C随之在边ON上运动,若CD=5,BC=24,运动过程中,点D到点O的最大距离为( )
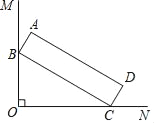
A. 24B. 25C. 3![]() +12D. 26
+12D. 26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道对于一个图形,通过不同的方法计算图形的面积时,可以得到一个数学等式.例如由图1可以得到![]() .请回答下列问题:
.请回答下列问题:

(1)写出图2中所表示的数学等式是 ;
(2)如图3,用四块完全相同的长方形拼成正方形,用不同的方法,计算图中阴影部分的面积,你能发现什么?(用含有![]() ,
,![]() 的式子表示) ;
的式子表示) ;
(3)通过上述的等量关系,我们可知: 当两个正数的和一定时,它们的差的绝对值越小,则积越 (填“ 大”“或“小”);当两个正数的积一定时,它们的差的绝对值越小,则和越 (填“ 大”或“小”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校计划在某商店购买秋季运动会的奖品,若买5个篮球和10个足球需花费1150元,若买9个篮球和6个足球需花费1170元.
(1)篮球和足球的单价各是多少元?
(2)实际购买时,正逢该商店进行促销.所有体育用品都按原价的八折优惠出售,学校购买了若干个篮球和足球,恰好花费1760元.请直接写出学校购买篮球和足球的个数各是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:如图1,在△ABC中,∠C=90°,分别以AC、BC为边向外侧作正方形ACDE和正方形BCFG.
(1)△ABC与△DCF面积的关系是;(请在横线上填写“相等”或“不相等”)
(2)拓展探究:若∠C≠90°,(1)中的结论还成立吗?若成立,请结合图2给出证明;若不成立,请说明理由;
(3)解决问题:如图3,在四边形ABCD中,AC⊥BD,且AC与BD的和为10,分别以四边形ABCD的四条边为边向外侧作正方形ABFE、正方形BCHG、正方形CDJI、正方形DALK,运用(2)的结论,图中阴影部分的面积和是否有最大值?如果有,请求出最大值,如果没有,请说明理由.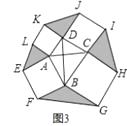
查看答案和解析>>
科目:初中数学 来源: 题型:
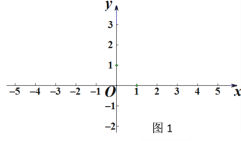
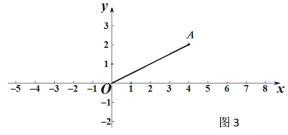
【题目】(1)尺规作图:如图1,请在x轴上作出表示(![]() ,0)的点(保留清晰作图痕迹,不写作法).
,0)的点(保留清晰作图痕迹,不写作法).
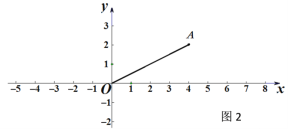
(2)如图2,已知点A(4,2),点B在x轴上,若∠OAB=90°,试求点B的坐标;
(3)如图3,已知点A(4,2),点C在x轴上,若△OAC为等腰三角形,试求点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com