
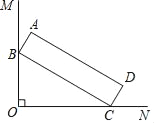
【题目】如图,∠MON=90°,长方形ABCD的顶点B、C分别在边OM、ON上,当B在边OM上运动时,C随之在边ON上运动,若CD=5,BC=24,运动过程中,点D到点O的最大距离为( )
A. 24B. 25C. 3![]() +12D. 26
+12D. 26
 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量(人) | 租金(元) | |
A | x | 45x | 400x |
B | 5-x |
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E为边CD上一点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F.若∠B=52°,∠DAE=20°,则∠FED′的大小为 . 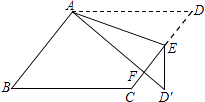
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.
(1)求A、B两种品牌服装每套进价分别为多少元?
(2)该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形A′B′C′是三角形ABC经过某种变换后得到的图形.
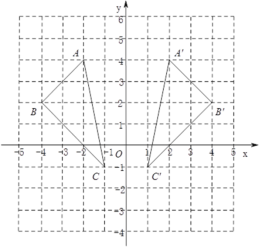
(1)分别写出点A和点A′,点B和点B′,点C和点C′的坐标;
(2)观察点A和点A′,点B和点B′,点C和点C′的坐标,用文字语言描述它们的坐标之间的关系 ;
(3)三角形ABC内任意一点M的坐标为(x,y),点M经过这种变换后得到点M′,则点M′的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
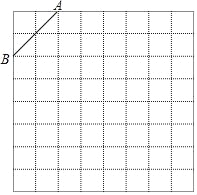
【题目】如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
(1)在网格中建立平面直角坐标系,使A点坐标为(﹣2,4),B点坐标为(﹣4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是 ;
(3)求△ABC中BC边上的高长.
查看答案和解析>>
科目:初中数学 来源: 题型:
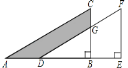
【题目】如图,将直角三角形 ABC 沿 AB 方向平移 AD 的长度得到三角形DEF,已知BE=5, EF=8, CG=2,则图中阴影部分的面积为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市决定购买A、B两种树苗对某段道路进行绿化改造,已知购买A种树苗9棵,B种树苗4棵,需要700元;购买A种树苗3棵,B种树苗5棵,则需要380元.
(1)求购买A、B两种树苗每颗各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗不能少于60棵,且用于购买这两种树苗的资金不能超过5260元.若购进这两种树苗共100棵,则有哪几种购买方案?哪种方案最省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com