
����Ŀ�����ⷢ�֣���ͼ1���ڡ�ABC�У���C=90�㣬�ֱ���AC��BCΪ���������������ACDE��������BCFG��
��1����ABC���DCF����Ĺ�ϵ���������ں�������д����ȡ�����ȡ���
��2����չ̽��������C��90�㣬��1���еĽ��ۻ�������������������ͼ2����֤����������������˵�����ɣ�
��3��������⣺��ͼ3�����ı���ABCD�У�AC��BD����AC��BD�ĺ�Ϊ10���ֱ����ı���ABCD��������Ϊ���������������ABFE��������BCHG��������CDJI��������DALK�����ã�2���Ľ��ۣ�ͼ����Ӱ���ֵ�������Ƿ������ֵ������У���������ֵ�����û�У���˵�����ɣ�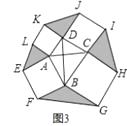
���𰸡�
��1�����
��2���⣺�������������£�
�ӳ�BC����P������A��AP��BP�ڵ�P������D��DQ��FC�ڵ�Q����ͼ��ʾ��
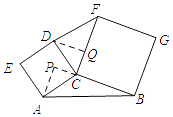
���APC=��DQC=90�㣮
���ı���ACDE��BCFG��Ϊ�����Σ�
��AC=CD��BC=CF����ACP+��PCD=90�㣬��DCQ+��PCD=90�㣬
���ACP=��DCQ��
�ڡ�APC�͡�DQC�У� 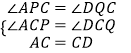 ��
��
��APC�ա�DQC��AAS����
��AP=DQ��
�֡�S��ABC= ![]() BCAP��S��DFC=
BCAP��S��DFC= ![]() FCDQ��
FCDQ��
��S��ABC=S��DFC��
��3���⣺ͼ����Ӱ���ֵ�����������ֵ���������£�
�ɣ�2���ã�S��AEL=S��ABD��S��BFG=S��ABC��S��CIH=S��CBD��S��DLK=S��DAC��
����Ӱ���ֵ����S=S��AEL+S��BFG+S��CIH+S��DLK=2S�ı���ABCD��
��AC=x����BD=10��x��
��AC��BD��
��S�ı���ABCD= ![]() AC��BD=
AC��BD= ![]() x��10��x��=��
x��10��x��=�� ![]() x2+5x=��
x2+5x=�� ![]() ��x��5��2+
��x��5��2+ ![]() ��
��
�ߩ� ![]() ��0��
��0��
��S�ı���ABCD�����ֵ�����ֵΪ ![]() ��
��
��ͼ����Ӱ���ֵ�����������ֵΪ25��
���������⣺��1����ȣ��������£�
���ı���ACDE���ı���BCFG�������Σ�
��AC=DC��BC=FC����ACD=��BCF=90�㣬
�ߡ�ACB=90�㣬
���DCF=90��=��ACB��
�ڡ�ABC���DFC�У� 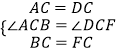 ��
��
���ABC�ա�DFC��AAS����
���ABC���DFC�������ȣ�
���Դ��ǣ���ȣ�
�����㾫����������Ҫ�����˶��κ�������ֵ�����֪ʶ�㣬��Ҫ��������Ա�����ȡֵ��Χ��ȫ��ʵ������ô�����ڶ��㴦ȡ�����ֵ������Сֵ��������x=-b/2aʱ��y��ֵ=(4ac-b2)/4a������ȷ�����⣮


 ��������������������ϵ�д�
��������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�������������ֱ�ΪA��1��1����B��4��2����C��3��4����
��1��������ABC����y��ĶԳ�ͼ�Ρ�A1B1C1����д����B1�����ꣻ
��2����x��������һ��P��ʹ��PAB���ܳ���С����ֱ��д����P�����꣮
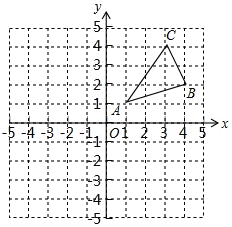
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
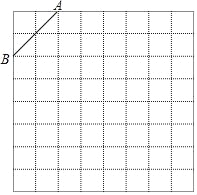
����Ŀ����ͼ�ǹ��Ϊ8��8�������������������������а�����Ҫ�������
(1)�������н���ƽ��ֱ������ϵ��ʹA������Ϊ(��2��4)��B������Ϊ(��4��2)��
(2)�ڵڶ������ڵĸ���ϻ�һ��C��ʹ��C���߶�AB���һ����ABΪ�ĵ��������Σ�������������������C���������� ����
(3)���ABC��BC���ϵĸ߳���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
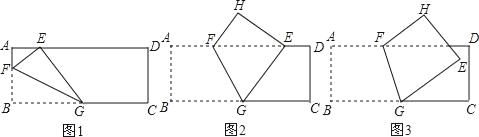
����Ŀ����ͼ��������ֽƬABCD�У�AB��8����ֽƬ�۵���ʹ����B���ڱ�AD�ϵ�E�㴦���ۺ۵�һ��G���ڱ�BC�ϣ�
(1)��ͼ1�����ۺ۵���һ��F��AB������AE��4ʱ����AF�ij�
(2)��ͼ2�����ۺ۵���һ��F��AD������BG��10ʱ��
����֤��EF��EG������AF�ij���
(3)��ͼ3�����ۺ۵���һ��F��AD���ϣ�B��Ķ�Ӧ��E�ڳ������ڲ���E��AD�ľ���Ϊ2cm����BG��10ʱ����AF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
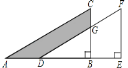
����Ŀ����ͼ����ֱ�������� ABC �� AB ����ƽ�� AD �ij��ȵõ�������DEF����֪BE=5�� EF=8�� CG=2����ͼ����Ӱ���ֵ����Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABC��������ABC����8��8�����У�λ����ͼ��ʾ��A����3��1����B����2��4����

��1�������ڷ����н���ֱ������ϵ����д��C������ꣻ
��2���ѡ�ABC����ƽ��1����λ���ȣ�������ƽ��2����λ���ȣ����㻭��ƽ�ƺ�ġ�A1B1C1������ABC�ڲ�һ��P������Ϊ��a��b�������P�Ķ�Ӧ��P1�������� ��
��3����x���ϴ���һ��D��ʹ��DB1C1���������3�������������ĵ�D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����л�������·��ͨ�����������涨:С�����ڳ��нֵ�����ʻ�ٶȲ��ó���70 km/h.��ͼ,һ��С������һ�����н�·��ֱ����ʻ,ijһʱ�̸պ���ʻ��·���泵�ټ������ǰ��30 m��,����2 s��,���С�����복�ټ���Ǽ����Ϊ50 m,����С������������?

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����C��DΪ��O�ϲ�ͬ��A��B�����㣬��ABD=2��BAC������C��CE��DB��DB���ӳ����ڵ�E��ֱ��AB��CE�ཻ�ڵ�F��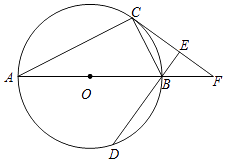
��1����֤��CFΪ��O�����ߣ�
��2����գ�����CAB�Ķ���Ϊʱ���ı���ACFD�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC=1����BAC=45�㣬��AEF���ɡ�ABC�Ƶ�A��˳ʱ�뷽����ת�õ���.����BE��CF�ཻ�ڵ�D.
��1����֤��BE=CF.
��2�����ı���ACDEΪ����ʱ����BD�ij�.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com