
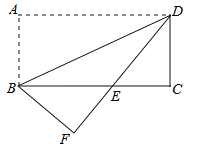
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.

【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)由AD∥BC,知∠ADB=∠DBC,根据折叠的性质∠ADB=∠BDF,所以∠DBC=∠BDF,得BE=DE,即可用AAS证△DCE≌△BFE;
(2)在Rt△BCD中,CD=2,∠ADB=∠DBC=30°,知BC=![]() ,在Rt△BCD中,CD=2,∠EDC=30°,知CE=
,在Rt△BCD中,CD=2,∠EDC=30°,知CE=![]() ,所以BE=BC﹣EC=
,所以BE=BC﹣EC=![]() .
.
试题解析:(1)∵AD∥BC,∴∠ADB=∠DBC,根据折叠的性质∠ADB=∠BDF,∠F=∠A=∠C=90°,∴∠DBC=∠BDF,∴BE=DE,在△DCE和△BFE中,∵∠BEF=∠DEC,∠F=∠C,BE=DE,∴△DCE≌△BFE;
(2)在Rt△BCD中,∵CD=2,∠ADB=∠DBC=30°,∴BC=![]() ,在Rt△BCD中,∵CD=2,∠EDC=30°,∴DE=2EC,∴
,在Rt△BCD中,∵CD=2,∠EDC=30°,∴DE=2EC,∴![]() ,∴CE=
,∴CE=![]() ,∴BE=BC﹣EC=
,∴BE=BC﹣EC=![]() .
.


科目:初中数学 来源: 题型:
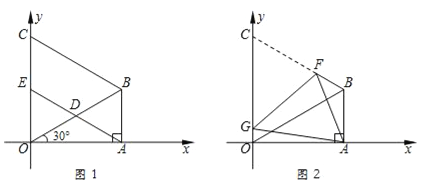
【题目】如图1,在△ABO中,∠OAB=90°,∠AOB=30°,OB=8.以OB为一边,在△OAB外作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E.
(1)求点B的坐标;
(2)求证:四边形ABCE是平行四边形;
(3)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设点A(m,n)在x轴上,且位于原点的左侧,则下列结论正确的是( )
A. m=0,n为一切数 B. m=0,n<0
C. m为一切数,n=0 D. m<0,n=0
查看答案和解析>>
科目:初中数学 来源: 题型:
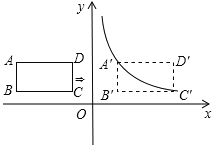
【题目】如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(![]() ,
,![]() ),AB=1,AD=2.
),AB=1,AD=2.
(1)直接写出B、C、D三点的坐标;
(2)将矩形ABCD向右平移m个单位,使点A、C恰好同时落在反比例函数![]() (
(![]() )的图象上,得矩形A′B′C′D′.求矩形ABCD的平移距离m和反比例函数的解析式.
)的图象上,得矩形A′B′C′D′.求矩形ABCD的平移距离m和反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( ) 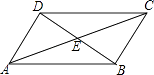
A.6
B.12
C.20
D.24
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com