
【题目】如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=8m,∠A=30°,则DE=m. 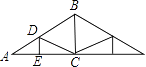
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (m为常数,﹣1≤m≤4).A(﹣m﹣1,
(m为常数,﹣1≤m≤4).A(﹣m﹣1,![]() ),B(
),B(![]() ,
,![]() ),C(﹣m,
),C(﹣m,![]() )是该抛物线上不同的三点,现将抛物线的对称轴绕坐标原点O逆时针旋转90°得到直线a,过抛物线顶点P作PH⊥a于H.
)是该抛物线上不同的三点,现将抛物线的对称轴绕坐标原点O逆时针旋转90°得到直线a,过抛物线顶点P作PH⊥a于H.
(1)用含m的代数式表示抛物线的顶点坐标;
(2)若无论m取何值,抛物线与直线y=x﹣km(k为常数)有且仅有一个公共点,求k的值;
(3)当1<PH≤6时,试比较![]() ,
,![]() ,
,![]() 之间的大小.
之间的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学活动课上,老师让同学们用两个大小、形状都相同的三角板画平行线AB,CD,并说出自己做法的依据.小琛、小萱、小冉三位同学的做法如下: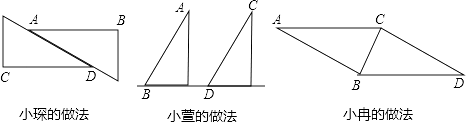
小琛说:“我的做法的依据是内错角相等,两直线平行.”
小萱做法的依据是 .
小冉做法的依据是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题为假命题的是( )
A. 三角形三个内角的和等于180° B. 三角形两边之和大于第三边
C. 三角形的外角大于任何一个和它不相邻的内角 D. 若a>0,b<0,则a+b>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节前夕,某商店根据市场调查,用1320元购进第一批盒装粽子,上市后很快售完,接着又用2880元购进第二批这种盒装粽子,已知第二批所购的粽子盒数是第一批所购粽子盒数的2倍,且每盒粽子的进价比第一批的进价多1元.
(1)第一批盒装粽子购进多少盒?
(2)若两批粽子按相同的标价销售,最后剩下50盒按八折优惠售出,如果两批粽子全部售出后利润不低于25%(不考虑其他因素),那么每盒粽子的标价至少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com