

分析 (1)运用Rt△ABE≌Rt△BCF,再利用角的关系求得∠BGE=90°求证;
(2)△BCF沿BF对折,得到△BPF,利用角的关系证明QF=QB,在Rt△QPB中,利用勾股定理即可解决问题.
(3)先求出正方形的边长,再根据面积比等于相似边长比的平方,求得S△AGN=$\frac{4}{5}$,再利用S四边形GHMN=S△AHM-S△AGN求解.
解答 (1)证明:如图1,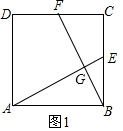
∵E,F分别是正方形ABCD边BC,CD的中点,
∴CF=BE,
在Rt△ABE和Rt△BCF中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠BCF}\\{BE=CF}\end{array}\right.$,
∴Rt△ABE≌Rt△BCF(SAS),
∠BAE=∠CBF,
又∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°,
∴∠BGE=90°,
∴AE⊥BF.
(2)解:如图2,根据题意得,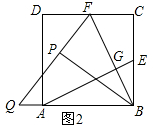
FP=FC,∠PFB=∠BFC,∠FPB=90°
∵CD∥AB,
∴∠CFB=∠ABF,
∴∠ABF=∠PFB,
∴QF=QB,
∵PF=FC=1,PB=BC=2,
在Rt△BPQ中,设QB=x,
∴x2=(x-1)2+22,
∴x=$\frac{5}{2}$,
∴AQ=BQ-AB=$\frac{5}{2}$-2=$\frac{1}{2}$.
(3)解:∵正方形ABCD的面积为4,
∴边长为2,
∵∠BAE=∠EAM,AE⊥BF,
∴AN=AB=2,
∵∠AHM=90°,
∴GN∥HM,
∴$\frac{{S}_{△AGN}}{{S}_{△AHM}}$=($\frac{AN}{AM}$ )2,
∴$\frac{{S}_{△AGN}}{1}$=( $\frac{2}{\sqrt{5}}$)2,
∴S△AGN=$\frac{4}{5}$,
∴S四边形GHMN=S△AHM-S△AGN=1-$\frac{4}{5}$=$\frac{1}{5}$,
∴四边形GHMN的面积是 $\frac{1}{5}$.
点评 本题考查的是旋转变换、翻折变换、正方形的性质、全等三角形的判定与性质等知识,熟知旋转、翻折不变性是解答此题的关键,学会构建方程解决问题,属于中考压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
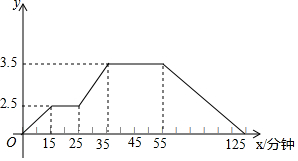 如图所示的图象反映的过程是:小强星期天从家跑步去体育场,在那里锻炼了一会儿后又走到文具店去买笔,然后步行回家,其中x表示时间,y表示小强离家的距离,根据图象回答下列问题.
如图所示的图象反映的过程是:小强星期天从家跑步去体育场,在那里锻炼了一会儿后又走到文具店去买笔,然后步行回家,其中x表示时间,y表示小强离家的距离,根据图象回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
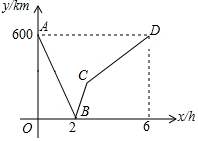 一列快车从甲驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,匀速行驶,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的关系,根据图象进行以下探究:
一列快车从甲驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,匀速行驶,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的关系,根据图象进行以下探究:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
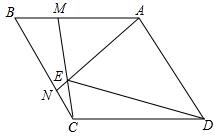 如图菱形ABCD中,∠ADC=60°,M、N分别为线段AB,BC上两点,且BM=CN,且AN,CM所在直线相交于E.
如图菱形ABCD中,∠ADC=60°,M、N分别为线段AB,BC上两点,且BM=CN,且AN,CM所在直线相交于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
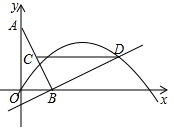 如图,A(0,2),B(1,0),点C为线段AB的中点,将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.
如图,A(0,2),B(1,0),点C为线段AB的中点,将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com