
【题目】用适当的方法解下列方程:
(1)x2=3x
(2)2x2﹣x﹣6=0.
(3)y2+3=2 ![]() y;
y;
(4)x2+2x﹣120=0.
【答案】
(1)
解:∵x2﹣3x=0,
∴x(x﹣3)=0,
则x=0或x﹣3=0,
解得:x=0或x=3
(2)
解:∵(x﹣2)(2x+3)=0,
∴x﹣2=0或2x+3=0,
解得:x=2或x=﹣ ![]()
(3)
解:∵y2﹣2 ![]() y+3=0,
y+3=0,
∴(y﹣ ![]() )2=0,
)2=0,
则y= ![]()
(4)
解:∵(x﹣10)(x+12)=0,
∴x﹣10=0或x+12=0,
解得:x=10或x=﹣12
【解析】(1)因式分解法求解可得;(2)因式分解法求解可得;(3)因式分解法求解可得;(4)因式分解法求解可得.
【考点精析】关于本题考查的因式分解法,需要了解已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,1),B(﹣1,1),C(﹣1,﹣2),D(1,﹣2),把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A→B→C→D→A…的规律绕在四边形ABCD的边上,则细线另一端所在位置的点的坐标是( )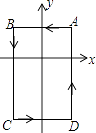
A.(﹣1,0)
B.(1,﹣2)
C.(1,1)
D.(0,﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售如下: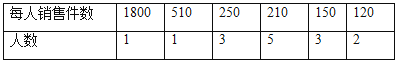
(1)求这15位营销人员该月销售量的平均数、中位数和众数.
(2)假设销售部负责人把每位营销员的月销售额定为320件,你认为是否合理?为什么?如不合理,请你制定一个合理的销售定额,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象与性质.
的图象与性质.
小军根据学习函数的经验, 对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小军的探究过程, 请补充完整:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是y与x的几组对应值:

在平面直角坐标系xOy中, 描出了以上表中各对对应值为坐标的点,根据描出的点, 画出该函数的图象;
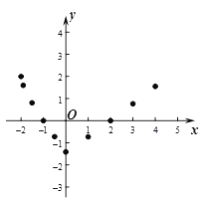
(3)观察图象,函数的最小值是 ;
(4)进一步探究,结合函数的图象, 写出该函数的一条性质(函数最小值除外): .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】病人按规定的剂量服用某种药物,测得服药后2小时,每毫升血液中的含药量达到最大值为4毫克.已知服药后,2小时前每毫升血液中的含药量y(毫克)与时间x(小时)成正比例,2小时后y与x成反比例(如图所示).根据以上信息解答下列问题. 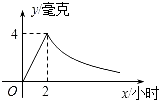
(1)求y与x之间的函数关系式;并写出自变量x的取值范围;
(2)若每毫升血液中的含药量不低于2毫克时治疗有效,那么病人服药一次治疗疾病的有效时间是多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB、CD被直线EF所截,FG平分∠EFD,∠1=∠2=80°,求∠BGF的度数. 解:因为∠1=∠2=80°(已知),
所以AB∥CD()
所以∠BGF+∠3=180°()
因为∠2+∠EFD=180°(邻补角的性质).
所以∠EFD= . (等式性质).
因为FG平分∠EFD(已知).
所以∠3=∠EFD(角平分线的性质).
所以∠3= . (等式性质).
所以∠BGF= . (等式性质).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc<0;②b2﹣4ac=0;③a>2;④4a﹣2b+c>0.其中正确结论的个数是( )
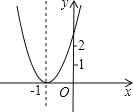
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.
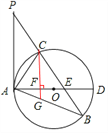
(1)求证:PA是⊙O的切线;
(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AGAB=48,求AC的长;
(3)在满足(2)的条件下,若AF:FD=1:2,GF=2,求⊙O的半径及sin∠ACE的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com