【题目】如图，矩形OABC的两边在坐标轴上，连接AC，抛物线y=x2-4x-2经过A，B两点．

（1）求A点坐标及线段AB的长；

（2）若点P由点A出发以每秒1个单位的速度沿AB边向点B移动，1秒后点Q也由点A出发以每秒7个单位的速度沿A-O-C-B的方向向点B移动，当其中一个点到达终点时另一个点也停止移动，点P的移动时间为t秒．

①当PQ⊥AC时，求t的值；

②当PQ∥AC时，对于抛物线对称轴上一点H，当点H的纵坐标满足条件_________时，∠HOQ＜∠POQ.（直接写出答案）

参考答案：

【答案】(1)、A(0，－2)；AB=4；(2)、①、t=；②、－2＜＜.

【解析】

试题分析：(1)、当x=0时求出y的值，即点A的坐标，根据矩形的性质得出点B的坐标，然后求出AB的长度；(2)、①、根据题意得出点A移动的路程，点Q的移动路程；②、当点Q在OA上时，PQ⊥AC，得出△QAP和△ABC相似，从而得出t的值，点Q在OC上时，得出t的值.

试题解析：(1)、抛物线,当x=0时，y=﹣2，∴A（0，﹣2）由于四边形OABC是矩形，所以AB∥x轴，即A、B的纵坐标相同；当时，，解得，

∴B（4，﹣2）. ∴AB=4.

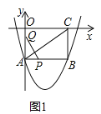
(2)、①、由题意知：A点移动路程为AP=t，Q点移动路程为.当Q点在OA上时，即，时，如图1，若PQ⊥AC， 则有Rt△QAP∽Rt△ABC.∴，即，

∴.∵，∴此时t值不合题意

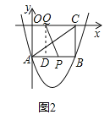
当Q点在OC上时，即，时， 如图2，过Q点作QD⊥AB.

∴AD=OQ=7（t﹣1）﹣2=7t﹣9. ∴DP=t﹣（7t﹣9）=9﹣6t.

若PQ⊥AC，则有Rt△QDP∽Rt△ABC，

∴，即，∴.∵，∴符合题意.

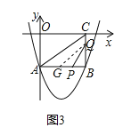
当Q点在BC上时，即，时， 如图3，若PQ⊥AC，过Q点作QG∥AC，

则QG⊥PG，即∠GQP=90°. ∴∠QPB＞90°.这与△QPB的内角和为180°矛盾，

此时PQ不与AC垂直 综上所述，当时，有PQ⊥AC.

②、.

关闭