
【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②当x>﹣1时,y随x增大而减小;③a+b+c<0;④若方程ax2+bx+c﹣m=0没有实数根,则m>2; ⑤3a+c<0.其中正确结论的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
【答案】C
【解析】(1)∵抛物线顶点(-1,2)在x轴上方,开口向下,
∴抛物线与x轴有两个交点,
∴![]() ,故①错误;
,故①错误;
(2)∵抛物线开口向下,对称轴为直线x=-1,
∴当x>-1时,y随x的增大而减小,故②正确;
(3)∵抛物线的对称轴为x=-1,
∴x=1时的函数值和x=-3时的函数值相等,
∴由图可知,a+b+c<0,故③正确;
(4)∵若方程ax2+bx+c﹣m=0没有实数根,
∴抛物线y=ax2+bx+c与直线y=m没有交点,
又∵抛物线y=ax2+bx+c开口向下,顶点坐标为(-1,2),
∴m>2,故④正确;
(5)∵抛物线的对称轴为直线![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,故⑤正确;
,故⑤正确;
综上所述,正确的结论有4个.
故选C.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明在数学课外小组活动时遇到这样一个问题:
![]()
如果一个不等式中含有绝对值,并且绝对值符号中含有未知数,我们把这个不等式叫做绝对值不等式,求绝对值不等式|x|>3的解集.
小明同学的思路如下:
先根据绝对值的定义,求出|x|恰好是3时x的值,并在数轴上表示为点A,B,如图所示.观察数轴发现,以点A,B为分界点把数轴分为三部分:
点A左边的点表示的数的绝对值大于3;
点A,B之间的点表示的数的绝对值小于3;
点B右边的点表示的数的绝对值大于3.
因此,小明得出结论绝对值不等式|x|>3的解集为:x<-3或x>3.
参照小明的思路,解决下列问题:
(1)请你直接写出下列绝对值不等式的解集.
①|x|>1的解集是 .
②|x|<2.5的解集是 .
(2)求绝对值不等式2|x-3|+5>13的解集.
(3)直接写出不等式x2>4的解集是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学1000名学生参加了“环保知识竞赛”,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)作为样本进行统计,并制作了如图频数分布表和频数分布直方图(不完整且局部污损,其中“■”表示被污损的数据).请解答下列问题:
成绩分组 | 频数 | 频率 |
50≤x<60 | 8 | 0.16 |
60≤x<70 | 12 | a |
70≤x<80 | ■ | 0.5 |
80≤x<90 | 3 | 0.06 |
90≤x<90 | b | c |
合计 | ■ | 1 |
(1)写出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)请估计这1000名学生中有多少人的竞赛成绩不低于70分;
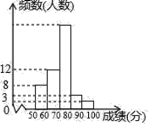
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠1+∠2=180°,∠B=∠D,CD平分∠ACF.
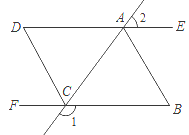
(1)DE与BF平行吗?请说明理由.
(2)AB与CD位置关系如何?为什么?
(3)AB平分∠CAE吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
中华优秀传统文化是中华民族的“根”和“魂”.为传承优秀传统文化,某校购进《西游记》和《三国演义》若干套,其中每套《西游记》的价格比每套《三国演义》的价格多40元,用3200元购买《三国演义》的套数是用2400元购买《西游记》套数的2倍,求每套《三国演义》的价格.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有大小两种货车,3辆大货车与2辆小货车一次可以运货21吨,2辆大货车与4辆小货车一次可以运货22吨.
(1)每辆大货车和每辆小货车一次各可以运货多少吨?
(2)现有这两种货车共10辆,要求一次运货不低于35吨,则其中大货车至少多少辆?(用不等式解答)
(3)日前有23吨货物需要运输,欲租用这两种货车运送,要求全部货物一次运完且每辆车必须装满.已知每辆大货车一次运货租金为300元,每辆小货车一次运货租金为200元,请列出所有的运输方案井求出最少租金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有三个分别写有数字1,2,3的小球,它们的形状、大小、质地等完全相同,先从盒子里随机取出一个小球,记下数字后放回盒子,摇匀后再随机取出一个小球,记下数字.请你用画树形图或列表的方法,求下列事件的概率:
(1)两次取出小球上的数字相同的概率;
(2)两次取出小球上的数字之和大于3的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论中:①OH∥BF,②GH=![]() BC,③BF=2OD,④∠CHF=45°.正确结论的个数为( )
BC,③BF=2OD,④∠CHF=45°.正确结论的个数为( )

A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,点D、E分别是边AB、AC上的两点(点D不与点A、 点B重合),且DE∥BC,以DE为一边,在四边形DBCE的内部作正方形DEFG,已知AB=AC=5,BC=6.
(1)试求△ABC的面积;
(2)当GF与BC重合时,求正方形DEFG的边长;
(3)若BG的长度等于正方形DEFG的边长,试求AD的长.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com