
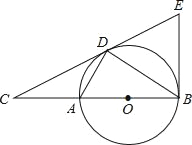
【题目】如图,点D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.(1)判断直线CD和⊙O的位置关系,并说明理由.
(2)过点B作⊙O的切线BE交直线CD于点E,若AC=2,⊙O的半径是3,求∠BEC的正切值.
【答案】(1)直线CD与⊙O的位置关系是相切.理由见解析;(2 )![]() .
.
【解析】【试题分析】
(1)证明切线的方法,知道直线与圆的交点,连接半径证垂直半径,即可.
(2)BC已知,关键是求BE 的长度,在Rt![]() 中,OA=5,OD=3,根据勾股定理得CD=4,在Rt
中,OA=5,OD=3,根据勾股定理得CD=4,在Rt![]() 中,设BE=DE=x,列出勾股定理方程(4+x)2=x2+(5+3)2,解得:x=6,所以tan∠BEC=
中,设BE=DE=x,列出勾股定理方程(4+x)2=x2+(5+3)2,解得:x=6,所以tan∠BEC=![]() .
.
【试题解析】
(1)直线CD与⊙O的位置关系是相切.
理由:
连接OD,如图所示:

∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠DBA=90°,
∵∠CDA=∠CBD,
∴∠DAB+∠CDA=90°,
∵OD=OA,
∴∠DAB=∠ADO,
∴∠CDA+∠ADO=90°,
即:OD⊥CE,
∴直线CD 是⊙O的切线.
即:直线CD 与⊙O的位置关系是相切.
(2)∵AC=2,⊙O的半径是3,
∴OC=2=3=5,OD=3,
在Rt△CDO中,由勾股定理得:CD=4.
∵CE切⊙O于D,EB切⊙O于B,
∴DE=EB,∠CBE=90°,
设DE=EB=x,
在Rt△CBE中,有勾股定理得:CE2=BE2+BC2,
则 (4+x)2=x2+(5+3)2,
解得:x=6,
即 BE=6,
∴tan∠BEC=![]() ,
,
即:tan∠BEC=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD(如图①)按如下步骤操作:(1)以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图②);(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图③);(3)将纸片展平,那么∠AFE的度数为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少;
(2)现在商城准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13000元,请分析合理的方案共有多少种,并确定获利最大的方案以及最大利润;
(3)实际进货时,厂家对电冰箱出厂价下调k(0<k<100)元,若商店保持这两种家电的售价不变,请你根据以上信息及(2)问中条件,设计出使这100台家电销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
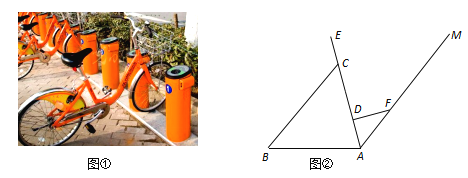
【题目】“低碳环保,你我同行”.近几年,各大城市的公共自行车给市民出行带来了极大的方便.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A.D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A.B.C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.

(1)求证:AP是⊙O的切线;
(2)求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a﹣2b,2﹣4ab)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴的对称点坐标为( )
A. (﹣3,7) B. (﹣1,7) C. (﹣4,10) D. (0,10)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A(-1,2)关于![]() 轴的对称点坐标是____________;点A关于原点的对称点的坐标是____________。点A关于x轴对称的点的坐标为____________
轴的对称点坐标是____________;点A关于原点的对称点的坐标是____________。点A关于x轴对称的点的坐标为____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com