
����Ŀ��ij�ҵ������̳ǵ��������ۼ�Ϊÿ̨2100Ԫ���յ������ۼ�Ϊÿ̨1750Ԫ��ÿ̨�����Ľ��۱�ÿ̨�յ��Ľ��۶�400Ԫ���̳���80000Ԫ������������������64000Ԫ�����յ���������ȣ�
��1����ÿ̨�������յ��Ľ��۷ֱ��Ƕ��٣�
��2�������̳���һ�ι��������ּҵ繲100̨���蹺�������x̨����100̨�ҵ������������ΪyԪ��Ҫ���յ����������������������2������������13000Ԫ������������ķ������ж����֣���ȷ���������ķ����Լ��������
��3��ʵ�ʽ���ʱ�����ҶԵ����������µ�k��0��k��100��Ԫ�����̵걣�������ּҵ���ۼ۲��䣬�������������Ϣ����2��������������Ƴ�ʹ��100̨�ҵ��������������Ľ���������
���𰸡���1��1600��2000����2����7�֣������������34̨���յ�66̨��������������Ϊ13300Ԫ����3����50��k��100ʱ�����������40̨���յ�60̨�������������0��k��50ʱ�����������34̨���յ�66̨�������������k=50ʱ��ÿ�ֽ���������������һ����
��������
��1����ÿ̨�յ��Ľ���ΪxԪ����ÿ̨�����Ľ���Ϊ��x+400��Ԫ���������̳���80000Ԫ������������������64000Ԫ�����յ���������������г����̣����ɽ��
��2���蹺�������x̨����100̨�ҵ������������ΪyԪ����ʾ��������y=��50x+15000����������ã����x��ȡֵ��Χ������xΪ������������x=34��35��36��37��38��39��40���������ķ�������7�֣�����һ�κ��������ʣ�ȷ���������ķ����Լ��������
��3���������������µ�k��0��k��100��Ԫʱ��������y=��k��50��x+15000��������������ۣ���k��50��0����k��50��0������һ�κ��������ʣ����ɽ��
�⣺��1����ÿ̨�յ��Ľ���ΪxԪ����ÿ̨�����Ľ���Ϊ��x+400��Ԫ����������ã�
![]() ����ã�x=1600��
����ã�x=1600��
�����飬x=1600��ԭ���̵Ľ⣬x+400=1600+400=2000��
��ÿ̨�յ��Ľ���Ϊ1600Ԫ����ÿ̨�����Ľ���Ϊ2000Ԫ��
��2���蹺�������x̨����100̨�ҵ������������ΪyԪ��
��y=��2100��2000��x+��1750��1600����100��x��=��50x+15000����������ã�
![]() ����ã�
����ã�![]() ��
��
��x����������x=34��35��36��37��38��39��40��
������ķ�������7�֣����ٵ����34̨���յ�66̨���ڵ����35̨���յ�65̨���۵����36̨���յ�64̨���ܵ����37̨���յ�63̨���ݵ����38̨���յ�62̨�������39̨���յ�61̨���ߵ����40̨���յ�60̨��
��y=��50x+15000��k=��50��0����y��x�����������
�൱x=34ʱ��y�����ֵ�����ֵΪ����50��34+15000=13300��Ԫ����
�𣺵����������34̨���յ�66̨��������������Ϊ13300Ԫ��
��3�������ҶԵ����������µ�k��0��k��100��Ԫ�����̵걣�������ּҵ���ۼ۲��䣬
������y=��2100��2000+k��x+��1750��1600����100��x��=��k��50��x+15000��
��k��50��0����50��k��100ʱ��y��x�����������
��![]() ��
��
�൱x=40ʱ����100̨�ҵ�����������������������40̨���յ�60̨��
��k��50��0����0��k��50ʱ��y��x���������С��
��![]() ��
��
�൱x=34ʱ����100̨�ҵ�����������������������34̨���յ�66̨��
�𣺵�50��k��100ʱ�����������40̨���յ�60̨�������������0��k��50ʱ�����������34̨���յ�66̨�������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
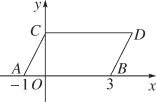
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ(��1��0)��(3��0)����ͬʱ��A��B��������ƽ��1����λ��������ƽ��2����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD��CD.
(1)���C��D�����ꣻ
(2)����P��ֱ��BD���˶�������PC��PO.
������P���߶�BD��(����B��D�غ�)ʱ����S��CDP��S��BOP��ȡֵ��Χ��
������P��ֱ��BD���˶�����̽����CPO����DCP����BOP�Ĺ�ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ����λΪ1�ķ���ֽ�ϣ���A1A2A3����A3A4A5����A5A6A7��������б����x���ϡ�б�߳��ֱ�Ϊ2��4��6�����ĵ���ֱ�������Σ�����A1A2A3�Ķ�������ֱ�ΪA1(2��0)��A2(1��-1)��A3(0��0)������ͼ����ʾ���ɣ�A2017�ĺ�����Ϊ�� ��

A. 1010 B. 2 C. 1 D. ��1006
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ѿ�֪��(a��b)2��0����a2��2ab+b2��0������a2+b2��2ab(���ҽ���a=bʱȡ�Ⱥ�)��
�Ķ�1����a��bΪʵ������a��0��b��0��
��(![]() )2��0����a��2
)2��0����a��2![]() +b��0����a+b��2
+b��0����a+b��2![]() (���ҽ���a=bʱȡ�Ⱥ�)��
(���ҽ���a=bʱȡ�Ⱥ�)��
�Ķ�2��������y=x![]() (m��0��x��0��mΪ����)�����Ķ�1���ۿ�֪��x
(m��0��x��0��mΪ����)�����Ķ�1���ۿ�֪��x![]() ��x
��x![]() ����x
����x![]() ��x2=m����x=
��x2=m����x=![]() (m��0)ʱ������y=x
(m��0)ʱ������y=x![]() ����СֵΪ2
����СֵΪ2![]() ��
��
�Ķ������������ݣ�����������⣺
����1����x��0ʱ��![]() ����СֵΪ������������x��0ʱ��
����СֵΪ������������x��0ʱ��![]() �����ֵΪ����������
�����ֵΪ����������
����2������y=a+![]() (a��1)����СֵΪ����������
(a��1)����СֵΪ����������
����3�������ʽ![]() (m����2)����Сֵ���������ʱ��m��ֵ��
(m����2)����Сֵ���������ʱ��m��ֵ��
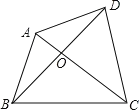
����4����ͼ���ı���ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����AOB����COD������ֱ�Ϊ4��16�����ı���ABCD�������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
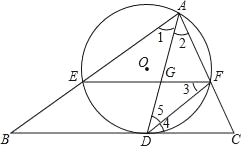
����Ŀ����ͼ��AD����ABC�Ľ�ƽ���ߣ���ADΪ�ҵ���O��AB��AC��E��F����֪EF��BC��
��1����֤��BC����O�����ߣ�
��2������֪AE=9��CF=4����DE����
��3���ڣ�2���������£�����BAC=60�㣬��tan��AFE��ֵ��GD����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������κ���y=x2-m������m��0����ͼ����x���·��IJ�����x�ᷭ�ۣ�ͼ������ಿ�ֱ��ֲ��䣬�γ��µ�ͼ���Ϊy1������һ�κ���y=x+b��ͼ���Ϊy2��������˵����
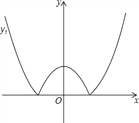
�ٵ�m=1����y1��y2ǡ������������ʱb��ΨһֵΪ1��
�ڵ�b=2����y1��y2ǡ����������ʱ��m��4��0��m��![]() ��
��
�۵�m=-bʱ��y1��y2һ���н��㣻
�ܵ�m=bʱ��y1��y2������2�����㣬������һ��Ϊ��0��m����
������ȷ˵�������Ϊ ______ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
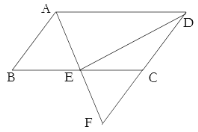
����Ŀ����ͼ��ƽ���ı���ABCD�У�AD=2AB��E��BC���е㣬����AE���ӳ���DC���ӳ����ڵ�F��
��1����֤��DE��AF��
��2������B=60����DE=4����AB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
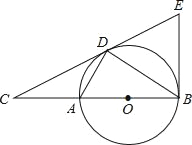
����Ŀ����ͼ����DΪ��O��һ�㣬��C��ֱ��BA���ӳ����ϣ�����CDA=��CBD����1���ж�ֱ��CD����O��λ�ù�ϵ����˵�����ɣ�
��2������B����O������BE��ֱ��CD�ڵ�E����AC=2����O�İ뾶��3������BEC������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�߶�![]() ��
�� ![]() �ڵ�
�ڵ�![]() ����
����![]() ��
�� ![]() ������
������![]() ��һ���㣬
��һ���㣬 ![]() ��
��![]() �ֱ���
�ֱ���![]() ��
�� ![]() ���е㣬����
���е㣬����![]() ��
�� ![]() ��
�� ![]() ��Բ��
��Բ��![]() ����һ����
����һ����![]() ����
����![]() ���߶�
���߶�![]() �ϣ�������
�ϣ�������![]() ��
�� ![]() ��
��

��![]() ����
����![]() ʱ����
ʱ����![]() �Ķ���Ϊ__________��
�Ķ���Ϊ__________��
��![]() ���ڵ�
���ڵ�![]() ���˶������У���
���˶������У���![]() ʱ��ȡ�ı���
ʱ��ȡ�ı���![]() һ�ߵ����˵���߶�
һ�ߵ����˵���߶�![]() ��һ��
��һ��![]() ������������Ϊ�������������ֱ�������Σ���
������������Ϊ�������������ֱ�������Σ���![]() ʱ����
ʱ����![]() ��ֵΪ__________��
��ֵΪ__________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com