
【题目】我们已经知道(a﹣b)2≥0,即a2﹣2ab+b2≥0.所以a2+b2≥2ab(当且仅当a=b时取等号).
阅读1:若a、b为实数,且a>0,b>0.
∵(![]() )2≥0,∴a﹣2
)2≥0,∴a﹣2![]() +b≥0,∴a+b≥2
+b≥0,∴a+b≥2![]() (当且仅当a=b时取等号).
(当且仅当a=b时取等号).
阅读2:若函数y=x![]() (m>0,x>0,m为常数).由阅读1结论可知:x
(m>0,x>0,m为常数).由阅读1结论可知:x![]() 即x
即x![]() ∴当x
∴当x![]() 即x2=m,∴x=
即x2=m,∴x=![]() (m>0)时,函数y=x
(m>0)时,函数y=x![]() 的最小值为2
的最小值为2![]() .
.
阅读理解上述内容,解答下列问题:
问题1:当x>0时,![]() 的最小值为 ;当x<0时,
的最小值为 ;当x<0时,![]() 的最大值为 .
的最大值为 .
问题2:函数y=a+![]() (a>1)的最小值为 .
(a>1)的最小值为 .
问题3:求代数式![]() (m>﹣2)的最小值,并求出此时的m的值.
(m>﹣2)的最小值,并求出此时的m的值.
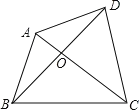
问题4:如图,四边形ABCD的对角线AC,BD相交于点O,△AOB、△COD的面积分别为4和16,求四边形ABCD面积的最小值.
【答案】(1)2,-2;(2)9;(3)最小值是4,m=0;(4)36.
【解析】
(1)当x>0时,按照公式a+b≥2![]() (当且仅当a=b时取等号)来计算即可;x<0时,由于x>0,
(当且仅当a=b时取等号)来计算即可;x<0时,由于x>0,![]() >0,则也可以按照公式a+b≥2
>0,则也可以按照公式a+b≥2![]() (当且仅当a=b时取等号)来计算;
(当且仅当a=b时取等号)来计算;
(2)将y=a+![]() 变形为y=a-1+
变形为y=a-1+![]() +1,故可根据公式a+b≥2
+1,故可根据公式a+b≥2![]() (当且仅当a=b时取等号)进行求解;
(当且仅当a=b时取等号)进行求解;
(3)将代数式![]() 变形得
变形得![]() ,故可根据公式a+b≥2
,故可根据公式a+b≥2![]() (当且仅当a=b时取等号)进行求解;
(当且仅当a=b时取等号)进行求解;
(4)设S△BOC=x,已知S△AOB=4,S△COD=16,则由等高三角形可知:S△BOC:S△COD=S△AOB:S△AOD,用含x的式子表示出S△AOD,四边形ABCD的面积用含x的代数式表示出来,再按照题中所给公式求得最小值,加上常数即可.
(1)当x>0时,![]() ≥2
≥2![]() =2;
=2;
当x<0时,![]() =(x
=(x![]() )
)
∵x![]() ≥2
≥2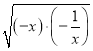 =2
=2
∴(x![]() )≤2
)≤2
∴当x>0时,x+![]() 的最小值为2;当x<0时,x+
的最小值为2;当x<0时,x+![]() 的最大值为2.
的最大值为2.
故答案为:2;2;
(2)y=a+![]() = a-1+
= a-1+![]() +1
+1
∵a-1>0
∴y=a-1+![]() +1≥
+1≥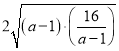 +1=2×4+1=9
+1=2×4+1=9
故答案为:9;
(3)![]() =
=![]()
∵m>﹣2,
∴![]() ≥
≥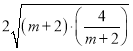 =4
=4
当m+2=![]() 时成立,即m=0(-4舍去)时,最小值为4.
时成立,即m=0(-4舍去)时,最小值为4.
(4)设S△BOC=x,已知S△AOB=4,S△COD=16
则由等高三角形可知:S△BOC:S△COD=S△AOB:S△AOD
∴x:16=4:S△AOD
∴S△AOD=![]()
∴四边形ABCD面积=4+16+x+![]() ≥20+
≥20+![]() =36
=36
当且仅当x=8时取等号,即四边形ABCD面积的最小值为36.


科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD(如图①)按如下步骤操作:(1)以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图②);(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图③);(3)将纸片展平,那么∠AFE的度数为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公大楼顶端A测得旗杆顶端E的俯角α是45°,旗杆低端D到大楼前梯砍底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:![]() ,则大楼AB的高度为_________米.
,则大楼AB的高度为_________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△AOB中,AO=AB,在直角坐标系中,点A的坐标是(2,2),点O的坐标是(0,0),将△AOB平移得到△A′O′B′,使得点A′在y轴上.点O′、B′在x轴上.则点B'的坐标是______

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是等边三角形ABC的高,点E是AD上的一个动点(点E不与点A重合),连接CE,将线段CE绕点E顺时针旋转60°得到EF,连接BF、CF.
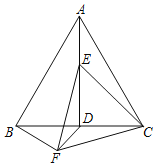
(1)猜想:△CEF是 三角形;
(2)求证:AE=BF;
(3)若AB=4,连接DF,在点E运动的过程中,请直接写出DF的最小值 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少;
(2)现在商城准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13000元,请分析合理的方案共有多少种,并确定获利最大的方案以及最大利润;
(3)实际进货时,厂家对电冰箱出厂价下调k(0<k<100)元,若商店保持这两种家电的售价不变,请你根据以上信息及(2)问中条件,设计出使这100台家电销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
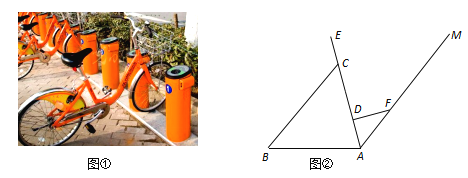
【题目】“低碳环保,你我同行”.近几年,各大城市的公共自行车给市民出行带来了极大的方便.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A.D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com