【题目】已知，如图，E、F 是平行四边形 ABCD 的对角线 AC 上的两点，AE=CF．
求证：（1）EB DF ；
（2）EB∥DF ．
习题精选系列答案科目：初中数学 来源： 题型：
【题目】在△ABC中，∠CAB＝2∠B，AE平分∠CAB，CD⊥AB于D，AC＝3，AD＝1.下列结论:①∠AEC＝∠CAB；②EF＝CE；③AC＝AE；④BD＝4；
正确的是___________(填序号)
查看答案和解析>>
科目：初中数学 来源： 题型：
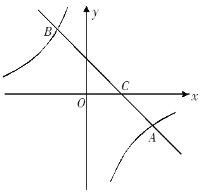
【题目】如图，在平面直角坐标系中，一次函数y =ax+b的图像与反比例函数y =
的图像交于A（4，﹣2）、B（﹣2，m）两点，与x轴交于点C.
（1）求a，m的值；
（2）请直接写出不等式ax+b≥的解集；
（3）点P在反比例函数图像上，且点P的横坐标为－4，在平面直角坐标系中是否存在一点Q，使得以A、B、P、Q为顶点的四边形为平行四边形？如果存在，请直接写出点Q的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在某月的日历上，圈出
，
，
，
，
，5个数，使它们呈一个十字架.
（1）如果它的和为55，求的值；
（2）如果它们的和为115，求D的值;
（3）这五个数的和可以是125吗？
查看答案和解析>>
科目：初中数学 来源： 题型：
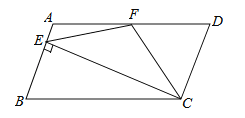
【题目】如图，在□ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上（E不与A、B重合），连接EF、CF，则下列结论中一定成立的是 ( )
①∠DCF=
∠BCD；②EF=CF；③
；④∠DFE=4∠AEF．
A. ①②③④ B. ①②③ C. ①② D. ①②④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】先阅读，后解答：
（1）由根式的性质计算下列式子得：
①
=3，②
，③
，④
=5，⑤
=0．
由上述计算，请写出
的结果（a为任意实数）．
（2）利用（1）中的结论，计算下列问题的结果：
①
；
②化简：
（x＜2）．
（3）应用：
若
=3，求x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
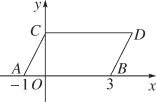
【题目】如图，在平面直角坐标系中，点A，B的坐标分别为(－1，0)，(3，0)，现同时将A，B两点向右平移1个单位，再向上平移2个单位，分别得到点A，B的对应点C，D，连接AC，BD，CD.
(1)求点C，D的坐标；
(2)若点P在直线BD上运动，连接PC，PO.
①若点P在线段BD上(不与B，D重合)时，求S△CDP＋S△BOP的取值范围；
②若点P在直线BD上运动，试探索∠CPO，∠DCP，∠BOP的关系，并证明你的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校八年级共有800名学生，准备调查他们对“低碳”知识的了解程度．
（1）在确定调查方式时，团委设计了以下三种方案：
方案一：调查八年级部分女生；
方案二：调查八年级部分男生；
方案三：到八年级每个班去随机调查一定数量的学生．
请问其中最具有代表性的一个方案是_____；
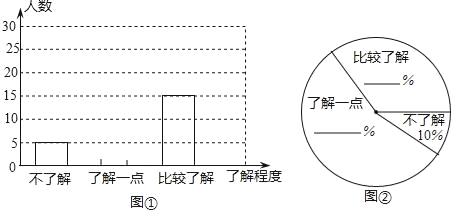
（2）团委采用了最具有代表性的调查方案，并用收集到的数据绘制出两幅不完整的统计图（如图①、图②所示），请你根据图中信息，将两个统计图补充完整；
（3）请你估计该校八年级约有多少名学生比较了解“低碳”知识．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们已经知道(a﹣b)2≥0，即a2﹣2ab+b2≥0．所以a2+b2≥2ab(当且仅当a=b时取等号)．
阅读1：若a、b为实数，且a＞0，b＞0．
∵(
)2≥0，∴a﹣2
+b≥0，∴a+b≥2(当且仅当a=b时取等号)．
阅读2：若函数y=x
(m＞0，x＞0，m为常数)．由阅读1结论可知：x
即x
∴当x
即x2=m，∴x=
(m＞0)时，函数y=x的最小值为2．
阅读理解上述内容，解答下列问题：
问题1：当x＞0时，
的最小值为 ；当x＜0时，的最大值为 ．
问题2：函数y=a+
(a＞1)的最小值为 ．
问题3：求代数式
(m＞﹣2)的最小值，并求出此时的m的值．
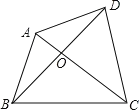
问题4：如图，四边形ABCD的对角线AC，BD相交于点O，△AOB、△COD的面积分别为4和16，求四边形ABCD面积的最小值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
