
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�һ�κ���y =ax+b��ͼ���뷴��������y =![]() ��ͼ����A��4����2����B����2��m�����㣬��x�ύ�ڵ�C.
��ͼ����A��4����2����B����2��m�����㣬��x�ύ�ڵ�C.
��1����a��m��ֵ��
��2����ֱ��д������ʽax+b��![]() �Ľ⼯��
�Ľ⼯��
��3����P�ڷ���������ͼ���ϣ��ҵ�P�ĺ�����Ϊ��4����ƽ��ֱ������ϵ���Ƿ����һ��Q��ʹ����A��B��P��QΪ������ı���Ϊƽ���ı��Σ�������ڣ���ֱ��д����Q������.
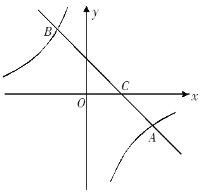
���𰸡�(1)a=��1��m=4��(2)x����2��0<x��4��(3)Q1(6��0) ��Q2(2��-4)��Q3 (-10��8).
��������
��1���Ƚ���A������뷴������������ʽ�����k�����������B���꣬���A��B�������ֱ�߽���ʽ�м������a��
��2������ͼ��ֱ�ӵó����ۣ�
��3���������P���꣬�����Q���꣬����ƽ���ı��εĶԽ�����ƽ�ֺ��е����깫ʽ������������⼴�ɵó����ۣ�
��1���ߵ�A��4����2���ڷ���������y��![]() �ϣ�
�ϣ�
��k��4������2������8��
�෴������������ʽΪy����![]() ��
��
�ߵ�B����2����m���ڷ����������ϣ�
�ੁ2m����8��
��m��4��
��B����2��4����
����A��4����2����B����2��4������ֱ��y��ax+b�У���
![]() ��
��
��![]() ��
��
����a����1��m��4��
��2����A��4����2����B����2��4����
���ʽax+b��![]() �Ľ⼯Ϊx����2��0��x��4��
�Ľ⼯Ϊx����2��0��x��4��
��3���ɣ�1��֪�������������Ľ���ʽΪy����![]() ��
��
�ߵ�P�ڷ���������ͼ���ϣ��Һ�����Ϊ��4��
���P��������Ϊ2��
��P����4��2����
���Q��c��n������A��B��P��QΪ������ı���Ϊƽ���ı��Σ�
�ٵ�ABΪ�Խ���ʱ��AB��PQ����ƽ�֣�
��![]() ��4��2����
��4��2����![]() ����4+c����
����4+c����![]() ����2+4����
����2+4����![]() ��2+n����
��2+n����
��c��6��n��0��
��Q��6��0����
�ڵ�APΪ�Խ���ʱ��AP��BQ����ƽ�֣�
��![]() ��4��4����
��4��4����![]() ����2+n����
����2+n����![]() ����2+2����
����2+2����![]() ��4+n����
��4+n����
��c��2��n����4��
��Q��2����4����
�۵�AQΪ�Խ���ʱ��AQ��BP����ƽ�֣�
��![]() ��4+c����
��4+c����![]() ����2��4����
����2��4����![]() ����2+n����
����2+n����![]() ��4+2����
��4+2����
��c����10��n��8��
��Q����10��8����
�������������ĵ�Q������Ϊ��6��0����2����4����10��8����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ�ķ���ֽ�У�С�����εĶ��������㣬![]() ��һ�����������(��
��һ�����������(��![]() ���������㶼�ڸ����)������Ҫ��ش���������:
���������㶼�ڸ����)������Ҫ��ش���������:
![]() ����
����![]() ������ƽ��6��������ƽ��
������ƽ��6��������ƽ��![]() �����õ�
�����õ�![]() ;
;
![]() ��������
��������![]() ��
��![]() ���ϵĸ�
���ϵĸ�![]() .
.
![]() ����
����![]() ��ֱ�ߣ���
��ֱ�ߣ���![]() �ֳ������ȵ�����������;
�ֳ������ȵ�����������;
![]() ������
������![]() ��һ�������ߣ�����
��һ�������ߣ�����![]() ȫ�ȵĸ��������.
ȫ�ȵĸ��������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ijʮ��·�ڵ������������ܼ���ֱ�У�Ҳ��������ת������ת���������������ǵȿ��ܵģ������������������ʮ��·��ʱ��
��1���������б�����״ͼ�ķ�������ʾ�����п��ܵĽ����
��2��������ȫ��ͬ����еĸ����� ������������������ת�ĸ����� ��
��3������ʮ��·���ҹ��䴦��ͨ���½����ÿ������ģ���˽��ܲ�����������ʻ�߷�ʱ�ζԳ���������ͳ�ƣ����������ڴ�ʮ��·������ת��Ƶ��Ϊ![]() ������ת��ֱ�е�Ƶ�ʾ�Ϊ
������ת��ֱ�е�Ƶ�ʾ�Ϊ![]() ��Ŀǰ�ڴ�·�ڣ�������ת����ת��ֱ�е��̵�����ʱ��ֱ�Ϊ30�룬���̵�����ʱ�䲻��������£�Ϊ�˻��⽻ͨӵ����������ͳ�Ƶ�֪ʶ�Դ�·������������̵�����ʱ�����������ĵ�����
��Ŀǰ�ڴ�·�ڣ�������ת����ת��ֱ�е��̵�����ʱ��ֱ�Ϊ30�룬���̵�����ʱ�䲻��������£�Ϊ�˻��⽻ͨӵ����������ͳ�Ƶ�֪ʶ�Դ�·������������̵�����ʱ�����������ĵ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����������ȫ��ͬ��������ֽƬABC��DEC�غϷ��ã�����![]() ��
��![]() .
.
��1����������
�ٹ̶�![]() ��ʹ
��ʹ![]() �Ƶ�C��ת.����Dǡ������AB����ʱ����ͼ2�����߶�DE��AC��λ�ù�ϵ��________����֤����
�Ƶ�C��ת.����Dǡ������AB����ʱ����ͼ2�����߶�DE��AC��λ�ù�ϵ��________����֤����
����![]() �����Ϊ
�����Ϊ![]() ��
��![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() ��������ϵ��________.
��������ϵ��________.
��2��������֤
��![]() �Ƶ�C��ת��ͼ3��ʾ��λ��ʱ��С�����루1����
�Ƶ�C��ת��ͼ3��ʾ��λ��ʱ��С�����루1����![]() ��
��![]() ��������ϵ��Ȼ����������ֱ�����
��������ϵ��Ȼ����������ֱ�����![]() ��
��![]() ��BC��CE���ϵĸߣ����ɴ�֤��С���IJ���.
��BC��CE���ϵĸߣ����ɴ�֤��С���IJ���.
��3����չ̽��
��֪![]() ����D�����ƽ������һ�㣬
����D�����ƽ������һ�㣬![]() ��
��![]() ��BC�ڵ�E����ͼ4��������������BA���Ƿ���ڵ�F��ʹ
��BC�ڵ�E����ͼ4��������������BA���Ƿ���ڵ�F��ʹ![]() �������ڣ���ֱ��д�����������ĵ�F�ĸ������������ڣ���˵������.
�������ڣ���ֱ��д�����������ĵ�F�ĸ������������ڣ���˵������.
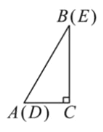
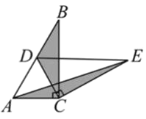
ͼ1 ͼ2
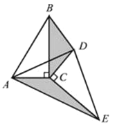
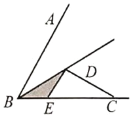
ͼ3 ͼ4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����ڳ�����һ���������壬���¶Ȳ���ʱ�������������ѹǿP��kPa�����������V��m3���ķ�������������ͼ����ͼ��ʾ��
��1������һ�����ı���ʽ��
��2��������ѹǿΪ48kPaʱ����V��ֵ��
��3���������ڵ����С��0.6m3ʱ������ը��Ϊ�˰�ȫ����������ѹǿ�����ڶ��٣�
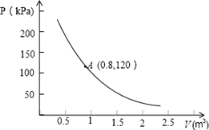
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ACDE��֤�����ɶ���ʱ�õ���һ��ͼ�Σ�a��b��c��Rt��ABC��Rt��BED�߳�����֪AE=![]() c����ʱ���ǰѹ���x������ax+
c����ʱ���ǰѹ���x������ax+![]() cx+b=0��һԪ���η��̳�Ϊ����ϵһԪ���η��̡�.
cx+b=0��һԪ���η��̳�Ϊ����ϵһԪ���η��̡�.

��������������
д��һ������ϵһԪ���η��̡���
��֤������x�ġ���ϵһԪ���η��̡�ax+![]() cx+b=0����ʵ������
cx+b=0����ʵ������
��x=1�ǡ���ϵһԪ���η��̡�ax+![]() cx+b=0��һ���������ı���ACDE���ܳ���
cx+b=0��һ���������ı���ACDE���ܳ���![]() ������ABC���.
������ABC���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��E��F ��ƽ���ı��� ABCD �ĶԽ��� AC �ϵ����㣬AE=CF��

��֤����1��EB DF ��
��2��EB��DF ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֽƬABCD����ͼ�٣������²����������1���Թ���A��ֱ��Ϊ�ۺ��۵�ֽƬ��ʹ��Bǡ������AD���ϣ��ۺ���BC�߽��ڵ�E����ͼ�ڣ�����2���Թ���E��ֱ��Ϊ�ۺ��۵�ֽƬ��ʹ��A����BC���ϣ��ۺ�EF��AD���ڵ�F����ͼ�ۣ�����3����ֽƬչƽ����ô��AFE�Ķ���Ϊ_________.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com