
ĄŸÌâÄżĄżÈçÍŒ1ŁŹœ«ÁœžöÍêÈ«ÏàÍŹ”ÄÈęœÇĐÎÖœÆŹABCșÍDECÖŰșÏ·ĆÖĂŁŹÆäÖĐ![]() ŁŹ
ŁŹ![]() .
.
Łš1Ł©ČÙŚś·ąÏÖ
ąÙč̶š![]() ŁŹÊč
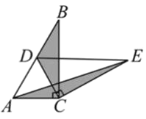
ŁŹÊč![]() ÈÆ”ăCĐęŚȘ.”±”ăDÇĄșĂÂäÔÚAB±ßÉÏʱŁšÈçÍŒ2Ł©Ł»Ï߶ÎDEÓëAC”ÄλÖĂčŰÏ”ÊÇ________ŁŹÇëրÜŁ»
ÈÆ”ăCĐęŚȘ.”±”ăDÇĄșĂÂäÔÚAB±ßÉÏʱŁšÈçÍŒ2Ł©Ł»Ï߶ÎDEÓëAC”ÄλÖĂčŰÏ”ÊÇ________ŁŹÇëրÜŁ»
ąÚÉè![]() ”ÄĂæ»ęÎȘ
”ÄĂæ»ęÎȘ![]() ŁŹ
ŁŹ![]() ”ÄĂæ»ęÎȘ
”ÄĂæ»ęÎȘ![]() ŁŹÔò
ŁŹÔò![]() Óë
Óë![]() ”ÄÊęÁżčŰÏ”ÊÇ________.
”ÄÊęÁżčŰÏ”ÊÇ________.
Łš2Ł©ČÂÏëÂÛÖ€
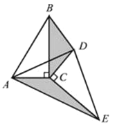
”±![]() ÈÆ”ăCĐęŚȘ”œÍŒ3ËùÊŸ”ÄλÖĂʱŁŹĐĄĂśČÂÏ룚1Ł©ÖĐ
ÈÆ”ăCĐęŚȘ”œÍŒ3ËùÊŸ”ÄλÖĂʱŁŹĐĄĂśČÂÏ룚1Ł©ÖĐ![]() Óë
Óë![]() ”ÄÊęÁżčŰÏ”ÈÔÈ»łÉÁąŁŹÇëÄă·Ö±đŚśłö
”ÄÊęÁżčŰÏ”ÈÔÈ»łÉÁąŁŹÇëÄă·Ö±đŚśłö![]() șÍ
șÍ![]() ÖĐBCĄąCE±ßÉÏ”ÄžßŁŹČąÓÉŽËրÜХÜ”ÄČÂÏë.
ÖĐBCĄąCE±ßÉÏ”ÄžßŁŹČąÓÉŽËրÜХÜ”ÄČÂÏë.
Łš3Ł©ÍŰŐčÌœŸż
ŒșÖȘ![]() ŁŹ”ăDÊÇÆäœÇÆœ·ÖÏßÉÏÒ»”㣏
ŁŹ”ăDÊÇÆäœÇÆœ·ÖÏßÉÏÒ»”㣏![]() ŁŹ
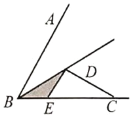
ŁŹ![]() œ»BCÓÚ”ăEŁšÈçÍŒ4Ł©ŁŹÇëÎÊÔÚÉäÏßBAÉÏÊÇ·ńŽæÔÚ”ăFŁŹÊč
œ»BCÓÚ”ăEŁšÈçÍŒ4Ł©ŁŹÇëÎÊÔÚÉäÏßBAÉÏÊÇ·ńŽæÔÚ”ăFŁŹÊč![]() ŁŹÈôŽæÔÚŁŹÇëÖ±œÓĐŽłö·ûșÏÌőŒț”Ä”ăF”ÄžöÊ꣏ÈôČ»ŽæÔÚŁŹÇë˔ÜÀíÓÉ.
ŁŹÈôŽæÔÚŁŹÇëÖ±œÓĐŽłö·ûșÏÌőŒț”Ä”ăF”ÄžöÊ꣏ÈôČ»ŽæÔÚŁŹÇë˔ÜÀíÓÉ.
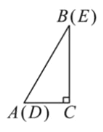
͌1 ͌2
͌3 ͌4
ĄŸŽđ°žĄżŁš1Ł©![]() ÀíÓÉŒûœâÎöŁŹ
ÀíÓÉŒûœâÎöŁŹ![]() Ł»Łš2Ł©ŒûœâÎöŁ»Łš3Ł©ŽæÔÚÁœžö.
Ł»Łš2Ł©ŒûœâÎöŁ»Łš3Ł©ŽæÔÚÁœžö.
ĄŸœâÎöĄż
Łš1Ł©ąÙžùŸĘĐęŚȘ”ÄĐÔÖÊżÉ”Ă![]() ŁŹÈ»șóÇółö
ŁŹÈ»șóÇółö![]() ÊǔȱßÈęœÇĐÎŁŹžùŸĘ”ȱßÈęœÇĐΔÄĐÔÖÊżÉ”Ă
ÊǔȱßÈęœÇĐÎŁŹžùŸĘ”ȱßÈęœÇĐΔÄĐÔÖÊżÉ”Ă![]() ŁŹÈ»șóžùŸĘÄÚŽíœÇÏà”ÈŁŹÁœÖ±ÏßÆœĐĐœâŽđŁ»
ŁŹÈ»șóžùŸĘÄÚŽíœÇÏà”ÈŁŹÁœÖ±ÏßÆœĐĐœâŽđŁ»
ąÚžùŸĘ”ȱßÈęœÇĐΔÄĐÔÖÊżÉ”ĂACŁœADŁŹÔÙžùŸĘÖ±œÇÈęœÇĐÎ30ĄăœÇËù¶Ô”ÄÖ±œÇ±ß”ÈÓÚб±ß”ÄÒ»°ëÇółöACŁœ![]() ABŁŹÈ»șóÇółöADŁœBDŁŹÔÙžùŸĘ”ȱßÈęœÇĐΔÄĐÔÖÊÇółö”ăC”œAB”ÄŸàÀë”ÈÓÚ”ăD”œAC”ÄŸàÀëŁŹÈ»șóžùŸĘ”È”Ś”Èžß”ÄÈęœÇĐΔÄĂæ»ęÏà”ÈœâŽđŁ»
ABŁŹÈ»șóÇółöADŁœBDŁŹÔÙžùŸĘ”ȱßÈęœÇĐΔÄĐÔÖÊÇółö”ăC”œAB”ÄŸàÀë”ÈÓÚ”ăD”œAC”ÄŸàÀëŁŹÈ»șóžùŸĘ”È”Ś”Èžß”ÄÈęœÇĐΔÄĂæ»ęÏà”ÈœâŽđŁ»
Łš2Ł©žùŸĘĐęŚȘ”ÄĐÔÖÊżÉ”ĂBCŁœCEŁŹACŁœCDŁŹÔÙÇółöĄÏACNŁœĄÏDCMŁŹÈ»șóÀûÓĂĄ°œÇœÇ±ßĄ±Ö€ĂśĄśACNșÍĄśDCMÈ«”ÈŁŹžùŸĘÈ«”ÈÈęœÇĐζÔÓŠ±ßÏà”ÈżÉ”ĂANŁœDMŁŹÈ»șóÀûÓĂ”È”Ś”Èžß”ÄÈęœÇĐΔÄĂæ»ęÏà”ÈրÜŁź
Łš3Ł©čę”ăDŚś![]() ŁŹÇółöËıßĐÎ
ŁŹÇółöËıßĐÎ![]() ÊÇÁâĐÎŁŹžùŸĘÁâĐΔĶԱßÏà”ÈżÉ”Ă
ÊÇÁâĐÎŁŹžùŸĘÁâĐΔĶԱßÏà”ÈżÉ”Ă![]() ŁŹÈ»șóžùŸĘ”È”Ś”Èžß”ÄÈęœÇĐΔÄĂæ»ęÏà”ÈżÉÖȘ”ă
ŁŹÈ»șóžùŸĘ”È”Ś”Èžß”ÄÈęœÇĐΔÄĂæ»ęÏà”ÈżÉÖȘ”ă![]() ÎȘËùÇó”Ĕ㣏čę”ăDŚś
ÎȘËùÇó”Ĕ㣏čę”ăDŚś![]() ŁŹÇółö
ŁŹÇółö![]() ŁŹŽÓ¶ű”Ă”œ
ŁŹŽÓ¶ű”Ă”œ![]() ÊǔȱßÈęœÇĐÎŁŹÈ»șóÇółö
ÊǔȱßÈęœÇĐÎŁŹÈ»șóÇółö![]() ŁŹÔÙÇółö
ŁŹÔÙÇółö![]() ŁŹÀûÓĂĄ°±ßœÇ±ßĄ±Ö€Ăś
ŁŹÀûÓĂĄ°±ßœÇ±ßĄ±Ö€Ăś![]() È«”ÈŁŹžùŸĘÈ«”ÈÈęœÇĐΔÄĂæ»ęÏà”ÈżÉ”Ă”ă
È«”ÈŁŹžùŸĘÈ«”ÈÈęœÇĐΔÄĂæ»ęÏà”ÈżÉ”Ă”ă![]() ÒČÊÇËùÇó”Ĕ㣟
ÒČÊÇËùÇó”Ĕ㣟
Łš1Ł©ąÙ![]() ŁŹ
ŁŹ
ÏÂĂæրÜŁșÓÉÌâÒâ![]() ŁŹÓÖÓÉĐęŚȘ”Ă
ŁŹÓÖÓÉĐęŚȘ”Ă![]() ŁŹ
ŁŹ
ËùÒÔ![]() ÊǔȱßÈęœÇĐÎ.
ÊǔȱßÈęœÇĐÎ.
ËùÒÔ![]() ŁŹÓÚÊÇ
ŁŹÓÚÊÇ![]() ŁŹËùÒÔ
ŁŹËùÒÔ![]() .
.
ąÚĄßACŁœ![]() ABŁŹADŁœACŁŹ
ABŁŹADŁœACŁŹ
ĄàADŁœBDŁŹ
Ąà![]()
ĄßDEĄÎACŁŹ
Ąà![]() ŁŹ
ŁŹ
Ąà![]() .
.
čÊŽđ°žÎȘŁșDEĄÎACŁŹ![]() Łź
Łź
Łš2Ł©ÈçÍŒŁŹ
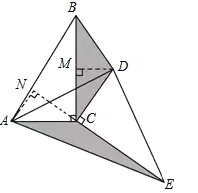
ĄßĄśDECÊÇÓÉĄśABCÈÆ”ăCĐęŚȘ”Ă”œŁŹ
ĄàBCŁœCEŁŹACŁœCDŁŹ
ĄßĄÏACNŁ«ĄÏBCNŁœ90ĄăŁŹĄÏDCMŁ«ĄÏBCNŁœ180Ąă90ĄăŁœ90ĄăŁŹ
ĄàĄÏACNŁœĄÏDCMŁŹ
ÔÚ![]() șÍ
șÍ![]() ÖĐŁŹ
ÖĐŁŹ
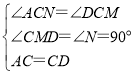 ŁŹ
ŁŹ
Ąà![]() ŁšAASŁ©ŁŹ
ŁšAASŁ©ŁŹ
ĄàANŁœDMŁŹ
ĄàĄśBDC”ÄĂæ»ęșÍĄśAEC”ÄĂæ»ęÏà”ÈŁš”È”Ś”Èžß”ÄÈęœÇĐΔÄĂæ»ęÏà”ÈŁ©ŁŹ
ŒŽ![]() Łź
Łź
Łš3Ł©ÈçÍŒŁŹčę”ăDŚś![]() œ»ABÓÚ
œ»ABÓÚ![]() Łź
Łź

Ąß![]() ŁŹ
ŁŹ
ĄàËıßĐÎ![]() ÊÇÆœĐĐËıßĐÎŁŹ
ÊÇÆœĐĐËıßĐÎŁŹ
ĄßĄÏABCŁœ60ĄăŁŹBDÆœ·ÖĄÏABCŁŹ
Ąà![]() ŁŹ
ŁŹ
Ąß![]() ŁŹ
ŁŹ
Ąà![]() ŁŹ
ŁŹ
Ąà![]() ŁŹ
ŁŹ
Ąà![]() ŁŹ
ŁŹ
ĄàËıßĐÎ![]() ÊÇÁâĐÎŁŹ
ÊÇÁâĐÎŁŹ
Ąà![]() ŁŹ
ŁŹ
ĄßBEĄą![]() ÉϔĞßÏà”ÈŁŹ
ÉϔĞßÏà”ÈŁŹ
Ąà![]() ,
,
Ąà”ă![]() ÊÇËùÇó”Ĕ㣻
ÊÇËùÇó”Ĕ㣻
čę”ăDŚś![]() ŁŹ
ŁŹ
Ąß![]() ,
,![]() ŁŹ
ŁŹ
Ąà![]()
Ąß![]() ŁŹ
ŁŹ
Ąà![]() ŁŹ
ŁŹ
Ąà![]() ÊǔȱßÈęœÇĐÎŁŹ
ÊǔȱßÈęœÇĐÎŁŹ
Ąà![]() ŁŹ
ŁŹ
ĄßBDŁœCDŁŹ
ĄàĄÏDBCŁœĄÏDCBŁœ30ĄăŁŹ
Ąà![]()
Ąà![]() ŁŹ
ŁŹ
![]() Łœ360Ąă150Ąă60ĄăŁœ150ĄăŁŹ
Łœ360Ąă150Ąă60ĄăŁœ150ĄăŁŹ
Ąà![]() ŁŹ
ŁŹ
ĄßÔÚ![]() șÍ
șÍ![]() ÖĐŁŹ
ÖĐŁŹ

Ąà![]() ŁšSASŁ©ŁŹ
ŁšSASŁ©ŁŹ
Ąà![]()
Ąß![]() ,
,
Ąà![]()
Ąà”ă![]() ÒČÊÇËùÇó”Ĕ㣏
ÒČÊÇËùÇó”Ĕ㣏
ĄàÔÚÉäÏßBAÉÏŽæÔÚ”ăF”ÄžöÊęÓĐÁœžö.


 żȘĐÄÍÜżÚËăÌâżšÏ”ÁĐŽđ°ž
żȘĐÄÍÜżÚËăÌâżšÏ”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÎȘÁËœâÎÒÊĐÊĐĂń2018ÄêłËŚűč«œ»ł””ÄĂżÈËÔŸù»š·ŃÇéżöŁŹÏàčŰČżĂĆËæ»ú”śČéÁË1000ÈË”ÄÏàčŰĐĆÏąŁŹČą»æÖÆÁËÈçÍŒËùÊŸ”ÄÆ”ÊęÖ±·œÍŒŁŹžùŸĘÍŒÖĐÌáč©”ÄĐĆÏąŁŹÓĐÏÂÁĐË”·šŁšĂżŚéÖ”°üÀšŚî”ÍÖ”ŁŹČ»°üÀšŚîžßÖ”Ł©ŁșąÙłËŚűč«œ»ł””ÄÔŸù»š·ŃÔÚ60ÔȘĄ«80ÔȘ”ÄÈËÊęŚî¶àŁ»ąÚÔŸù»š·ŃÔÚ160ÔȘŁšșŹ160ÔȘŁ©ÒÔÉÏ”ÄÈËÊęŐŒËù”śČéŚÜÈËÊę”Ä10%Ł»ąÛÔÚËù”śČé”Ä1000ÈËÖĐŁŹÖÁÉÙÓĐÒ»°ëÒÔÉÏ”ÄÈË”ÄÔŸù»š·ŃłŹčę75ÔȘŁ»ąÜÎȘÁËÈĂÊĐĂńÏíÊÜžü¶à”ÄÓƻʣŹÏàčŰČżĂĆÄâÈ·¶šÒ»žöŐÛżÛ±êŚŒŁŹŒÆ»źÊč30%ŚóÓÒ”ÄÈË»ń”ĂÓƻʣŹÄÇĂŽżÉÒÔÊdzˌűč«œ»ł””ÄÔŸù»š·ŃŽï”œ100ÔȘŁšșŹ100ÔȘŁ©ÒÔÉÏ”ÄÈËÏíÊÜŐÛżÛŁź

A.1žöB.2žöC.3žöD.4žö
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÔÚĄśABCÖĐŁŹĄÏCABŁœ2ĄÏBŁŹAEÆœ·ÖĄÏCABŁŹCDĄÍABÓÚDŁŹACŁœ3ŁŹADŁœ1.ÏÂÁĐœáÂÛ:ąÙĄÏAECŁœĄÏCABŁ»ąÚEFŁœCEŁ»ąÛACŁœAEŁ»ąÜBDŁœ4Ł»

ŐęÈ·”ÄÊÇ___________(ÌîĐòșĆ)
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
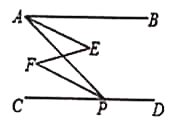
ĄŸÌâÄżĄżÈçÍŒŁŹĄ°șÍĐłșĆĄ±žßÌúÁĐł””ÄĐĄŚÀ°ćÊŐÆđʱŁŹĐĄŚÀ°ć”ÄÖ§ŒÜ”Ś¶ËÓëŚÀĂ涄¶Ë”ÄŸàÀëOAŁœ75ÀćĂŚŁŹÇÒżÉÒÔœüËÆżŽŚśÓë”ŰĂæŽčÖ±ŁźŐčżȘĐĄŚÀ°ćÊčŚÀĂæ±ŁłÖËźÆœŁŹŽËʱCBĄÍAOŁŹĄÏAOBŁœĄÏACBŁœ37ĄăŁŹÇÒÖ§ŒÜł€OBÓëŚÀĂæżíBC”Äł€¶ÈÖźșÍ”ÈÓÚOA”Äł€¶ÈŁźÇóĐĄŚÀ°ćŚÀĂæ”Äżí¶ÈBCŁźŁšČÎżŒÊęŸĘ![]() ŁŹ
ŁŹ ![]() ŁŹ
ŁŹ ![]() Ł©
Ł©

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÔÚÆœĂæÖ±œÇŚű±êÏ”![]() ÖĐŁŹĆŚÎïÏß
ÖĐŁŹĆŚÎïÏß![]() Ÿčę”ă
Ÿčę”ă![]() ŁŹÇÒÓë
ŁŹÇÒÓë![]() Öá”ÄÒ»žöœ»”ăÎȘ
Öá”ÄÒ»žöœ»”ăÎȘ![]() Łź
Łź
Łš1Ł©ÇóĆŚÎïÏß![]() ”ıíŽïÊœŁ»
”ıíŽïÊœŁ»
Łš2Ł©![]() ÊÇĆŚÎïÏß
ÊÇĆŚÎïÏß![]() Óë
Óë![]() Öá”ÄÁíÒ»žöœ»”㣏”ă
Öá”ÄÁíÒ»žöœ»”㣏”ă![]() ”ÄŚű±êÎȘ
”ÄŚű±êÎȘ![]() ŁŹÆäÖĐ
ŁŹÆäÖĐ![]() ŁŹĄś
ŁŹĄś![]() ”ÄĂæ»ęÎȘ
”ÄĂæ»ęÎȘ![]() Łź
Łź
ąÙÇó![]() ”ÄÖ”Ł»
”ÄÖ”Ł»
ąÚœ«ĆŚÎïÏß![]() ÏòÉÏÆœÒÆ
ÏòÉÏÆœÒÆ![]() žö”„λŁŹ”Ă”œĆŚÎïÏß
žö”„λŁŹ”Ă”œĆŚÎïÏß![]() ŁźÈô”±
ŁźÈô”±![]() ʱŁŹĆŚÎïÏß
ʱŁŹĆŚÎïÏß![]() Óë
Óë![]() ÖáÖ»ÓĐÒ»žöč«čȔ㣏œáșÏșŻÊę”ÄÍŒÏóŁŹÇó
ÖáÖ»ÓĐÒ»žöč«čȔ㣏œáșÏșŻÊę”ÄÍŒÏóŁŹÇó![]() ”ÄÈĄÖ”·¶Î§Łź
”ÄÈĄÖ”·¶Î§Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÍêłÉÏÂĂæ”ÄրÜ.
ÈçÍŒĄą![]() Óë
Óë![]() »„Č裏
»„Č裏![]() ŁŹÇóÖ€Łș
ŁŹÇóÖ€Łș![]() .¶ÔÓÚ±ŸÌâĐĄÀöÊÇŐâŃùրܔģŹÇëÄăœ«Ëę”ÄրÜčęłÌČčłäÍêŐû.
.¶ÔÓÚ±ŸÌâĐĄÀöÊÇŐâŃùրܔģŹÇëÄăœ«Ëę”ÄրÜčęłÌČčłäÍêŐû.
րÜŁș![]() Óë
Óë![]() »„Č裏(ÒŃÖȘ)
»„Č裏(ÒŃÖȘ)
![]() .(________________________________)
.(________________________________)
![]() .(________________________________)
.(________________________________)
![]() ŁŹ(ÒŃÖȘ)
ŁŹ(ÒŃÖȘ)
![]() ŁŹ(”ÈÁżŽú»»)
ŁŹ(”ÈÁżŽú»»)
ŒŽ_______________=_______________.
![]() .(________________________________)
.(________________________________)
![]() .(________________________________)
.(________________________________)
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
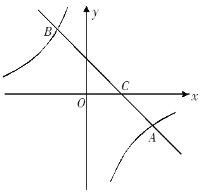
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹÒ»ŽÎșŻÊęy =ax+b”ÄÍŒÏńÓë·Ž±ÈÀęșŻÊęy =![]() ”ÄÍŒÏńœ»ÓÚAŁš4ŁŹ©2Ł©ĄąBŁš©2ŁŹmŁ©Áœ”㣏ÓëxÖ᜻ÓÚ”ăC.
”ÄÍŒÏńœ»ÓÚAŁš4ŁŹ©2Ł©ĄąBŁš©2ŁŹmŁ©Áœ”㣏ÓëxÖ᜻ÓÚ”ăC.
Łš1Ł©ÇóaŁŹm”ÄÖ”Ł»
Łš2Ł©ÇëÖ±œÓĐŽłöČ»”ÈÊœax+bĄĘ![]() ”ÄœâŒŻŁ»
”ÄœâŒŻŁ»
Łš3Ł©”ăPÔÚ·Ž±ÈÀęșŻÊęÍŒÏńÉÏŁŹÇÒ”ăP”ÄșáŚű±êÎȘŁ4ŁŹÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐÊÇ·ńŽæÔÚÒ»”ăQŁŹÊč”ĂÒÔAĄąBĄąPĄąQÎȘ¶„”ă”ÄËıßĐÎÎȘÆœĐĐËıßĐÎŁżÈçčûŽæÔÚŁŹÇëÖ±œÓĐŽłö”ăQ”ÄŚű±ê.
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚÄłÔ”ÄÈŐÀúÉÏŁŹÈŠłö![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ5žöÊ꣏ÊčËüĂÇłÊÒ»žöÊźŚÖŒÜ.
ŁŹ5žöÊ꣏ÊčËüĂÇłÊÒ»žöÊźŚÖŒÜ.

Łš1Ł©ÈçčûËü”ÄșÍÎȘ55ŁŹÇó![]() ”ÄÖ”Ł»
”ÄÖ”Ł»
Łš2Ł©ÈçčûËüĂÇ”ÄșÍÎȘ115ŁŹÇóD”ÄÖ”;
Łš3Ł©ŐâÎćžöÊę”ÄșÍżÉÒÔÊÇ125ÂđŁż
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÄłĐŁ°ËÄꌶčČÓĐ800ĂûѧÉúŁŹŚŒ±ž”śČéËûĂǶԥ°”ÍÌŒĄ±ÖȘʶ”ÄÁËœâłÌ¶ÈŁź
Łš1Ł©ÔÚÈ·¶š”śČ鷜ʜʱŁŹÍĆÎŻÉèŒÆÁËÒÔÏÂÈęÖÖ·œ°žŁș
·œ°žÒ»Łș”śČé°ËÄêŒ¶Čż·ÖĆźÉúŁ»
·œ°ž¶țŁș”śČé°ËÄêŒ¶Čż·ÖÄĐÉúŁ»
·œ°žÈęŁș”œ°ËÄêŒ¶Ăżžö°àÈ„Ëæ»ú”śČéÒ»¶šÊęÁż”ÄѧÉúŁź
ÇëÎÊÆäÖĐŚîŸßÓĐŽú±íĐÔ”ÄÒ»žö·œ°žÊÇ_____Ł»
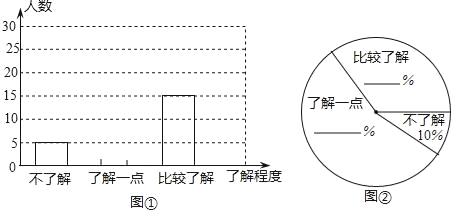
Łš2Ł©ÍĆÎŻČÉÓĂÁËŚîŸßÓĐŽú±íĐԔĔśČé·œ°žŁŹČąÓĂÊŐŒŻ”œ”ÄÊęŸĘ»æÖÆłöÁœ·ùČ»ÍêŐû”ÄÍłŒÆÍŒŁšÈçÍŒąÙĄąÍŒąÚËùÊŸŁ©ŁŹÇëÄăžùŸĘÍŒÖĐĐĆÏąŁŹœ«ÁœžöÍłŒÆÍŒČčłäÍêŐûŁ»
Łš3Ł©ÇëÄăčÀŒÆžĂĐŁ°ËÄꌶԌÓжàÉÙĂûѧÉú±ÈœÏÁËœâĄ°”ÍÌŒĄ±ÖȘʶŁź
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com