
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() ,且与
,且与![]() 轴的一个交点为
轴的一个交点为![]() .
.
(1)求抛物线![]() 的表达式;
的表达式;
(2)![]() 是抛物线
是抛物线![]() 与
与![]() 轴的另一个交点,点
轴的另一个交点,点![]() 的坐标为
的坐标为![]() ,其中
,其中![]() ,△
,△![]() 的面积为
的面积为![]() .
.
①求![]() 的值;
的值;
②将抛物线![]() 向上平移
向上平移![]() 个单位,得到抛物线
个单位,得到抛物线![]() .若当
.若当![]() 时,抛物线
时,抛物线![]() 与
与![]() 轴只有一个公共点,结合函数的图象,求
轴只有一个公共点,结合函数的图象,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②答案见解析.
;②答案见解析.
【解析】试题分析:(1)将A、B的坐标代入抛物线解析式求出b、c即可;(2)①过A作AF⊥x轴与点F,如图1,首先求出D的坐标,再根据△ADE的面积可求出DE的长度,接着可求出OE的长度即m的值;②利用抛物线的平移变换,可设抛物线C2的表达式为y=(x-1)2-4+n,接下去分类讨论:求出抛物线过点E和过原点时对应的n的值,并画出图像,利用图像可确定n的范围;当抛物线顶点再x轴上时,求出n的值.综上得到n的取值范围.
试题解析:
(1)∵抛物线C1:y=x2+bx+c经过点A(2,-3),且与x轴的一个交点为B(3,0),
∴![]() ,
,
解得![]() ,
,
∴抛物线C1解析式为y=x2-2x-3;
(2)
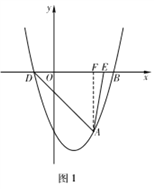
①过A作AF⊥x轴与点F,如图1,
∵y=x2-2x-3=(x-1)2-4,
∴抛物线对称轴为:x=1,
∴D(-1,0),
∵E(m,0),m>0,
∴S△ADE=![]() DE·AF=
DE·AF=![]() DE×3=
DE×3=![]() ,
,
∴DE=![]() ,
,
∴m=OE=DE-OD=![]() .
.
②
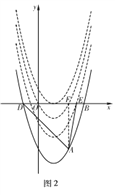
设抛物线C2的表达式为y=(x-1)2-4+n,
如图2,当抛物线C2经过E(![]() ,0)时,
,0)时,
(![]() -1)2-4+n=0,解得n=
-1)2-4+n=0,解得n=![]() ;
;
当抛物线C2经过原点时,
(0-1)2-4+n=0,解得n=3;
∵0≤x≤![]() 时,抛物线C2与x轴只有一个公共点,
时,抛物线C2与x轴只有一个公共点,
∴结合图像可知,当![]() ≤n<3时,符合题意.
≤n<3时,符合题意.
令y=0,(x-1)2-4+n=0,
由题意得,b2-4ac=16-4n=0,解得n=4.
综上, ![]() ≤n<3或n=4.
≤n<3或n=4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】“全民阅读”深入人心,好读书,读好书,让人终身受益.为满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和动漫书两类图书.经了解,20本文学名著和40本动漫书共需1560元,20本文学名著比20本动漫书多360元(注:所采购的文学名著价格都一样,所采购的动漫书价格都一样).
(1)求每本文学名著和动漫书各多少元?
(2)若学校要求购买动漫书比文学名著多20本,动漫书和文学名著总数不低于74本,总费用不超过2100,请求出所有符合条件的购书方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
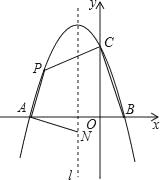
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种情况是等可能的,当三辆汽车经过这个十字路口时:
(1)请你用列表或画树状图的方法,表示出所有可能的结果;
(2)三辆车全部同向而行的概率是 ,至少有两辆车向左转的概率是 ;
(3)由于十字路口右拐弯处是通往新建经济开发区的,因此交管部门在汽车行驶高峰时段对车流量作了统计,发现汽车在此十字路口向右转的频率为![]() ,向左转和直行的频率均为
,向左转和直行的频率均为![]() .目前在此路口,汽车左转、右转、直行的绿灯亮的时间分别为30秒,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整.
.目前在此路口,汽车左转、右转、直行的绿灯亮的时间分别为30秒,在绿灯亮总时间不变的条件下,为了缓解交通拥挤,请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整.
查看答案和解析>>
科目:初中数学 来源: 题型:
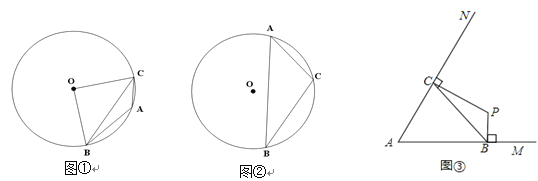
【题目】已知A、B、C三点不在同一直线上.
(1)若点A、B、C均在半径为R的⊙O上,
①如图①,当∠A=135°,R=1时,求∠BOC的度数和BC的长.
②如图②,当∠A为锐角时,求证: ![]() ;
;
(2)若定长线段BC的两个端点分别在∠MAN的两边AM、AN(B、C均与A不重合)滑动,如图③,当∠MAN=60°,BC=2时,分别作BP⊥AM,CP⊥AN,交点为P,试探索在整个滑动过程中,P、A两点间的距离是否保持不变?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中![]() ,
,![]() .
.
(1)操作发现
①固定![]() ,使
,使![]() 绕点C旋转.当点D恰好落在AB边上时(如图2);线段DE与AC的位置关系是________,请证明;
绕点C旋转.当点D恰好落在AB边上时(如图2);线段DE与AC的位置关系是________,请证明;
②设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 的数量关系是________.
的数量关系是________.
(2)猜想论证
当![]() 绕点C旋转到图3所示的位置时,小明猜想(1)中
绕点C旋转到图3所示的位置时,小明猜想(1)中![]() 与
与![]() 的数量关系仍然成立,请你分别作出
的数量关系仍然成立,请你分别作出![]() 和
和![]() 中BC、CE边上的高,并由此证明小明的猜想.
中BC、CE边上的高,并由此证明小明的猜想.
(3)拓展探究
己知![]() ,点D是其角平分线上一点,
,点D是其角平分线上一点,![]() ,
,![]() 交BC于点E(如图4),请问在射线BA上是否存在点F,使
交BC于点E(如图4),请问在射线BA上是否存在点F,使![]() ,若存在,请直接写出符合条件的点F的个数,若不存在,请说明理由.
,若存在,请直接写出符合条件的点F的个数,若不存在,请说明理由.
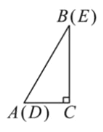
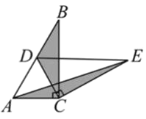
图1 图2
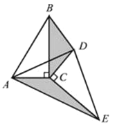
图3 图4
查看答案和解析>>
科目:初中数学 来源: 题型:
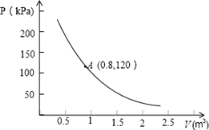
【题目】某气球内充满了一定量的气体,当温度不变时,气球内气体的压强P(kPa)是气体体积V(m3)的反比例函数,其图像如图所示.
(1)求这一函数的表达式;
(2)当气体压强为48kPa时,求V的值?
(3)当气球内的体积小于0.6m3时,气球将爆炸,为了安全起见,气体的压强不大于多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防疾病,某单位对办公室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成为正比例,药物燃烧后,y与x成反比例(如图),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量6毫克,请根据题中所提供的信息,解答下列问题:

(1)药物燃烧时,y关于x的函数关系式为________,自变量x的取值范为________;药物燃烧后,y关于x的函数关系式为________.
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时员工方可进办公室,那么从消毒开始,至少需要经过________分钟后,员工才能回到办公室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com