
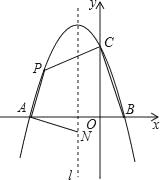
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
【答案】(1)y=﹣(x+1)2+4,顶点坐标为(﹣1,4);(2)①点P(﹣![]() ﹣1,2);②P(﹣
﹣1,2);②P(﹣![]() ,
, ![]() )
)
【解析】试题分析:(1)将B、C的坐标代入已知的抛物线的解析式,由对称轴为![]() 即可得到抛物线的解析式;
即可得到抛物线的解析式;
(2)①首先求得抛物线与x轴的交点坐标,然后根据已知条件得到PD=OA,从而得到方程求得x的值即可求得点P的坐标;
②![]() ,表示出来得到二次函数,求得最值即可.
,表示出来得到二次函数,求得最值即可.
试题解析:(1)∵抛物线![]() 与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为
与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为![]() ,∴
,∴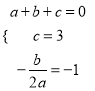 ,解得:
,解得: 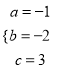 ,∴二次函数的解析式为
,∴二次函数的解析式为![]() =
=![]() ,∴顶点坐标为(﹣1,4);
,∴顶点坐标为(﹣1,4);
(2)令![]() ,解得
,解得![]() 或
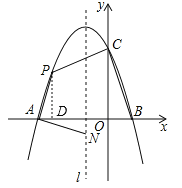
或![]() ,∴点A(﹣3,0),B(1,0),作PD⊥x轴于点D,∵点P在
,∴点A(﹣3,0),B(1,0),作PD⊥x轴于点D,∵点P在![]() 上,∴设点P(x,
上,∴设点P(x, ![]() ),
),
①∵PA⊥NA,且PA=NA,∴△PAD≌△AND,∴OA=PD,即![]() ,解得x=
,解得x=![]() (舍去)或x=
(舍去)或x=![]() ,∴点P(
,∴点P(![]() ,2);
,2);
②设P(x,y),则![]() ,∵
,∵![]()
=![]() OBOC+
OBOC+![]() ADPD+
ADPD+![]() (PD+OC)OD=
(PD+OC)OD=![]() =
= ![]()
=![]() =
=![]() =
=![]() ,
,
∴当x=![]() 时,
时, ![]() =
=![]() ,当x=
,当x=![]() 时,
时, ![]() =
=![]() ,此时P(
,此时P(![]() ,
, ![]() ).
).


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
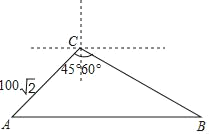
【题目】在某校组织的“交通安全宣传教育月”活动中,八年级数学兴趣小组的同学进行了如下的课外实践活动.具体内容如下:在一段笔直的公路上选取两点A、B,在公路另一侧的开阔地带选取一观测点C,在C处测得点A位于C点的南偏西45°方向,且距离为100![]() 米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒.
米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒.
(1)请你帮助他们算一算,这辆小车是否超速?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,计算结果保留两位小数).
≈1.73,计算结果保留两位小数).
(2)请你以交通警察叔叔的身份对此小轿车的行为作出处理意见,并就乡村公路安全管理提出自己的建议。(处理意见合情合理,建议尽量全面。)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:如图1,若![]() ,则
,则![]() .
.
理由:如图,过点![]() 作
作![]() ,
,
则![]() .
.
因为![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() .
.

交流:(1)若将点![]() 移至图2所示的位置,
移至图2所示的位置,![]() ,此时
,此时![]() 、
、![]() 、
、![]() 之间有什么关系?请说明理由.
之间有什么关系?请说明理由.
探究:(2)在图3中,![]() ,
,![]() 、
、![]() 又有何关系?
又有何关系?
应用:(3)在图4中,若![]() ,又得到什么结论?请直接写出该结论.
,又得到什么结论?请直接写出该结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,E为正方形ABCD的边BC延长线上一点,且CE=AC,AE交CD于点F,那么∠AFC的度数为( )
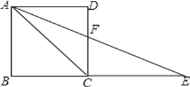
A. 112.5° B. 125° C. 135° D. 150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有三个点![]() ,
,![]() 是
是![]() 的边
的边![]() 上一点,
上一点,![]() 经平移后得到
经平移后得到![]() ,点
,点![]() 的对应点为
的对应点为![]() .
.
(1)画出平移后的![]() ,写出点
,写出点![]() 的坐标;
的坐标;
(2)![]() 的面积为_________________;
的面积为_________________;
(3)若点![]() 是
是![]() 轴上一动点,
轴上一动点,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的关系式(用含
之间的关系式(用含![]() 的式子表示
的式子表示![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠CAB=2∠B,AE平分∠CAB,CD⊥AB于D,AC=3,AD=1.下列结论:①∠AEC=∠CAB;②EF=CE;③AC=AE;④BD=4;

正确的是___________(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() ,且与
,且与![]() 轴的一个交点为
轴的一个交点为![]() .
.
(1)求抛物线![]() 的表达式;
的表达式;
(2)![]() 是抛物线
是抛物线![]() 与
与![]() 轴的另一个交点,点
轴的另一个交点,点![]() 的坐标为
的坐标为![]() ,其中
,其中![]() ,△
,△![]() 的面积为
的面积为![]() .
.
①求![]() 的值;
的值;
②将抛物线![]() 向上平移
向上平移![]() 个单位,得到抛物线
个单位,得到抛物线![]() .若当
.若当![]() 时,抛物线
时,抛物线![]() 与
与![]() 轴只有一个公共点,结合函数的图象,求
轴只有一个公共点,结合函数的图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上(E不与A、B重合),连接EF、CF,则下列结论中一定成立的是 ( )
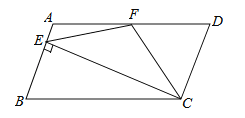
①∠DCF=![]() ∠BCD;②EF=CF;③
∠BCD;②EF=CF;③![]() ;④∠DFE=4∠AEF.
;④∠DFE=4∠AEF.
A. ①②③④ B. ①②③ C. ①② D. ①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com