
【题目】阅读材料:如图1,若![]() ,则
,则![]() .
.
理由:如图,过点![]() 作
作![]() ,
,
则![]() .
.
因为![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() .
.

交流:(1)若将点![]() 移至图2所示的位置,
移至图2所示的位置,![]() ,此时
,此时![]() 、
、![]() 、
、![]() 之间有什么关系?请说明理由.
之间有什么关系?请说明理由.
探究:(2)在图3中,![]() ,
,![]() 、
、![]() 又有何关系?
又有何关系?
应用:(3)在图4中,若![]() ,又得到什么结论?请直接写出该结论.
,又得到什么结论?请直接写出该结论.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
![]() .
.
【解析】
(1)过点E作EF∥AB,由平行线的性质可知∠B+∠BEF=180°,∠D+∠DEF=180°,再由角之间的关系即可得出结论;
(2)过点F作FM∥AB,用(1)的结论可知∠E=∠B+∠EFM,∠G=∠GFM+∠D,再由角之间的关系即可得出结论;
(3)已知AB∥CD,连接AB、CD的折线内折或外折,或改变E点位置、或增加折线的条数,通过适当地改变其中的一个条件,就能得出新的结论,给我们创造性的思考留下了极大的空间,解题的关键是过E点作AB(或CD)的平行线,把复杂的图形化归为基本图形.
(1)过点E作EF∥AB,如图2所示.
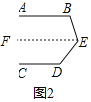
∵AB∥EF,
∴∠B+∠BEF=180°,
∵EF∥AB∥CD,
∴∠D+∠DEF=180°,
∴∠B+∠BEF+∠D+∠DEF=180°+180°,
∵∠E=∠BEF+∠DEF,
∴∠B+∠D+∠E=360°.
(2)过点F作FM∥AB,如图3所示.
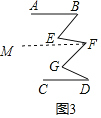
∵AB∥FM,结合(1)结论,
∴∠E=∠B+∠EFM,
∵FM∥AB∥CD,结合(1)结论,
∴∠G=∠GFM+∠D,
又∵∠F=∠EFM+∠GFM,
∴∠E+∠G=∠B+∠D+∠F.
(3)如图:
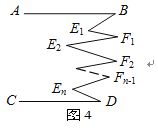
根据(1)和(2)中的结论,我们得到两条平行线之间,内折的所有角的度数之和等于外折的所有角的度数之和,即:
![]()
![]() .
.


科目:初中数学 来源: 题型:
【题目】某地要建造一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰在水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,抛物线形状如图(1)所示.图(2)建立直角坐标系,水流喷出的高度y(米)与水平距离x(米)之间的关系是![]() .请回答下列问题:
.请回答下列问题:

(1)柱子OA的高度是多少米?
(2)喷出的水流距水平面的最大高度是多少米?
(3)若不计其他因素,水池的半径至少要多少米才能使喷出的水流不至于落在池外?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①表示的是某综合商场今年1~5月的商品各月销售总额的情况,图②表示的是商场服装部各月销售额占商场当月销售总额的百分比情况,观察图①、图②,解答下列问题:
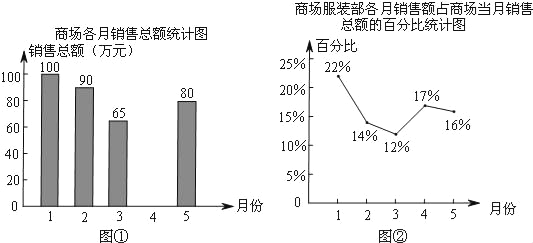
(1)来自商场财务部的数据报告表明,商场1~5月的商品销售总额一共是410万元,请你根据这一信息将图①中的统计图补充完整;
(2)商场服装部5月份的销售额是多少万元?
(3)小刚观察图②后认为,5月份商场服装部的销售额比4月份减少了.你同意他的看法吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“全民阅读”深入人心,好读书,读好书,让人终身受益.为满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和动漫书两类图书.经了解,20本文学名著和40本动漫书共需1560元,20本文学名著比20本动漫书多360元(注:所采购的文学名著价格都一样,所采购的动漫书价格都一样).
(1)求每本文学名著和动漫书各多少元?
(2)若学校要求购买动漫书比文学名著多20本,动漫书和文学名著总数不低于74本,总费用不超过2100,请求出所有符合条件的购书方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初三综合素质评定结束后,为了了解年级的评定情况,现对初三某班的学生进行了评定等级的调查,绘制了如下男女生等级情况折线统计图和全班等级情况扇形统计图.

(1)调查发现评定等级为合格的男生有2人,女生有1人,则全班共有 名学生.
(2)补全女生等级评定的折线统计图.
(3)根据调查情况,该班班主任从评定等级为合格和A的学生中各选1名学生进行交流,请用树形图或表格求出刚好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的方格纸中,小正方形的顶点叫做格点,![]() 是一个格点三角形(即
是一个格点三角形(即![]() 的三个顶点都在格点上),根据要求回答下列问题:
的三个顶点都在格点上),根据要求回答下列问题:
![]() 画出
画出![]() 先向左平移6格,再向上平移
先向左平移6格,再向上平移![]() 格所得的
格所得的![]() ;
;
![]() 利用网格画出
利用网格画出![]() 中
中![]() 边上的高
边上的高![]() .
.
![]() 过点
过点![]() 画直线,将
画直线,将![]() 分成面积相等的两个三角形;
分成面积相等的两个三角形;
![]() 画出与
画出与![]() 有一条公共边,且与
有一条公共边,且与![]() 全等的格点三角形.
全等的格点三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形AEFG的顶点E,G分别在正方形ABCD的AB,AD边上,连接B,交EF于点M,交FG于点N,设AE=a,AG=b,AB=c(b<a<c).
(1)求证: ![]() ;
;
(2)求△AMN的面积(用a,b,c的代数式表示);
(3)当∠MAN=45°时,求证:c2=2ab.

查看答案和解析>>
科目:初中数学 来源: 题型:
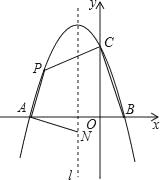
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
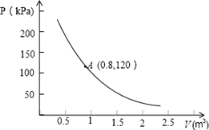
【题目】某气球内充满了一定量的气体,当温度不变时,气球内气体的压强P(kPa)是气体体积V(m3)的反比例函数,其图像如图所示.
(1)求这一函数的表达式;
(2)当气体压强为48kPa时,求V的值?
(3)当气球内的体积小于0.6m3时,气球将爆炸,为了安全起见,气体的压强不大于多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com