
【题目】图①表示的是某综合商场今年1~5月的商品各月销售总额的情况,图②表示的是商场服装部各月销售额占商场当月销售总额的百分比情况,观察图①、图②,解答下列问题:
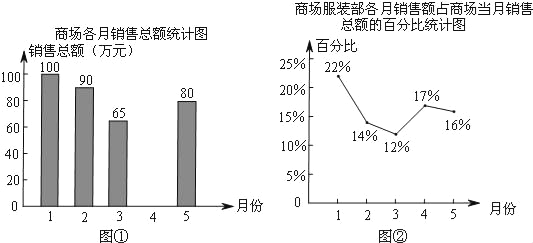
(1)来自商场财务部的数据报告表明,商场1~5月的商品销售总额一共是410万元,请你根据这一信息将图①中的统计图补充完整;
(2)商场服装部5月份的销售额是多少万元?
(3)小刚观察图②后认为,5月份商场服装部的销售额比4月份减少了.你同意他的看法吗?请说明理由.
【答案】(1)75;(2)12.8万元;(3)小刚的说法是错误的
【解析】试题分析:(1)销售总额减去已知各月的销售额,即可得到4月份的销售额;
(2)商场服装部5月份的销售额=5月份的销售总额×服装部5月份销售额占当月销售总额的百分比;
(3)分别求出服装部4月份和5月份的销售额,比较大小即可得出结论.
试题解析:解:(1)410﹣(100+90+65+80)=410﹣335=75,补全图形如下:
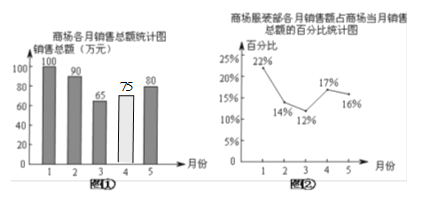
(2)商场服装部5月份的销售额是:80万元×16%=12.8万元;
(3)不同意小刚的说法,理由如下:
4月和5月的销售额分别是75万元和80万元,服装销售额各占当月的17%和16%,
则服装部4月份的销售额为75×17%=12.75万元,5月份的销售额为80×16%=12.8万元,
12.75<12.8,
故小刚的说法是错误的.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,BE为∠ABC的角平分线交AC于E,交AD于F,FG∥BD,交AC于G,过E作EH⊥CD于H,连接FH,下列结论:①四边形CHFG是平行四边形,②AE=CG,③FE=FD,④四边形AFHE是菱形,其中正确的是( )
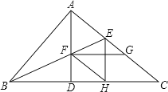
A.①②③④ B.②③④ C.①③④ D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在线段OA,OC上,且OB=OD,∠1=∠2,AE=CF.
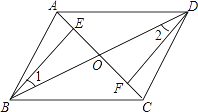
(1)证明:△BEO≌△DFO;
(2)证明:四边形ABCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
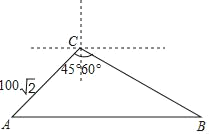
【题目】在某校组织的“交通安全宣传教育月”活动中,八年级数学兴趣小组的同学进行了如下的课外实践活动.具体内容如下:在一段笔直的公路上选取两点A、B,在公路另一侧的开阔地带选取一观测点C,在C处测得点A位于C点的南偏西45°方向,且距离为100![]() 米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒.
米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒.
(1)请你帮助他们算一算,这辆小车是否超速?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,计算结果保留两位小数).
≈1.73,计算结果保留两位小数).
(2)请你以交通警察叔叔的身份对此小轿车的行为作出处理意见,并就乡村公路安全管理提出自己的建议。(处理意见合情合理,建议尽量全面。)
查看答案和解析>>
科目:初中数学 来源: 题型:
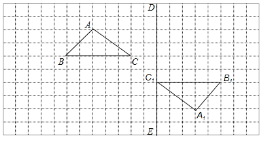
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(三角形顶点是网格线的交点)和△A1B1C1,且△ABC与△A1B1C1,成中心对称.
(1)画出△ABC和△A1B1C1的对称中心![]() ;
;
(2)将△A1B1C1沿直线![]() 方向向上平移6格,得到△A2B2C2,画出△A2B2C2;
方向向上平移6格,得到△A2B2C2,画出△A2B2C2;
(3)将△A2B2C2绕点C2顺时针方向旋转90°,得到△A3B3C3,画出△A3B3C3.
查看答案和解析>>
科目:初中数学 来源: 题型:
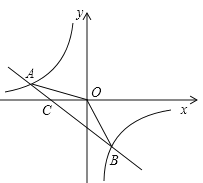
【题目】如图,已知A(-4,![]() )、B(2,-4)是一次函数
)、B(2,-4)是一次函数![]() 的图象和反比例函数
的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与![]() 轴的交点C的坐标及△AOB的面积;
轴的交点C的坐标及△AOB的面积;
(3)求方程![]() 的解(直接写出答案)
的解(直接写出答案)
(4)求不等式![]() 的解集(直接写出答案)
的解集(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
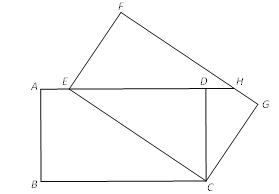
【题目】如图,将矩形ABCD绕点C旋转得到矩形FECG,点E在AD上,延长ED交FG于点H.
(1)求证:△EDC≌△HFE;
(2)连接BE、CH.
①四边形BEHC是怎样的特殊四边形?证明你的结论.
②当AB与BC的比值为 时,四边形BEHC为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:如图1,若![]() ,则
,则![]() .
.
理由:如图,过点![]() 作
作![]() ,
,
则![]() .
.
因为![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() .
.

交流:(1)若将点![]() 移至图2所示的位置,
移至图2所示的位置,![]() ,此时
,此时![]() 、
、![]() 、
、![]() 之间有什么关系?请说明理由.
之间有什么关系?请说明理由.
探究:(2)在图3中,![]() ,
,![]() 、
、![]() 又有何关系?
又有何关系?
应用:(3)在图4中,若![]() ,又得到什么结论?请直接写出该结论.
,又得到什么结论?请直接写出该结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com