
����Ŀ����֪A��B��C���㲻��ͬһֱ����.
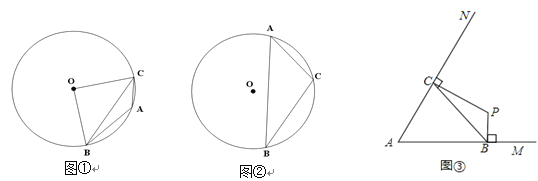
��1������A��B��C���ڰ뾶ΪR�ġ�O����
����ͼ��������A=135����R=1ʱ�����BOC�Ķ�����BC�ij���
����ͼ�ڣ�����AΪ���ʱ����֤�� ![]() ��
��
��2���������߶�BC�������˵�ֱ��ڡ�MAN������AM��AN��B��C����A���غϣ���������ͼ�ۣ�����MAN=60����BC=2ʱ���ֱ���BP��AM��CP��AN������ΪP����̽�����������������У�P��A�����ľ����Ƿֲ��䣿��˵�����ɣ�
���𰸡���1���١�BOC=90����BC=![]() ����֤������������2�����������������У�P��A�����ľ����Ƿֲ��䣬���ɼ�������
����֤������������2�����������������У�P��A�����ľ����Ƿֲ��䣬���ɼ�������
�������������������1���ٸ���ͬ�����Ե�Բ�ܽ���Բ�Ľǵ�һ�룬��Ϊ��A=135���������Ż����ԵĽǡ�BOC=270���������ӻ�BC���Եġ�BOC=90�������ɹ��ɶ��������BC�ij��ȣ����ӳ�CO��![]() O�ڵ�E������BE�����ԡ�A=��E����ΪCEΪ
O�ڵ�E������BE�����ԡ�A=��E����ΪCEΪ![]() 0��ֱ�����ó���CBE=90��������sinA=sinE=
0��ֱ�����ó���CBE=90��������sinA=sinE=![]() =
=![]() ����2������AP��ȡAP���е�K���ֱ�����CK��BK������BP��AM��CP��AN����KH��BC��BC�ڵ�H������ֱ������������б���ϵ����ߵ���б�ߵ�һ�룬��CK=BK=AK=PK������A��B��P��C����KΪԲ�ģ�
����2������AP��ȡAP���е�K���ֱ�����CK��BK������BP��AM��CP��AN����KH��BC��BC�ڵ�H������ֱ������������б���ϵ����ߵ���б�ߵ�һ�룬��CK=BK=AK=PK������A��B��P��C����KΪԲ�ģ� ![]() APΪ�뾶��Բ�ϣ��������߶�BC�������˵�ֱ��ڡ�MAN������AM��AN��B��C����A���غϣ���������ͼ������MAN=60ʱ����BKC=120��BC=2������BKC��һ������Ϊ120�����ױ�BC=2�ĵ��������Σ��������CK=BK=
APΪ�뾶��Բ�ϣ��������߶�BC�������˵�ֱ��ڡ�MAN������AM��AN��B��C����A���غϣ���������ͼ������MAN=60ʱ����BKC=120��BC=2������BKC��һ������Ϊ120�����ױ�BC=2�ĵ��������Σ��������CK=BK=![]() AP=
AP=![]() ����AP=
����AP=![]() ���������������������У�P��A�����ľ��뱣�ֲ��䣮
���������������������У�P��A�����ľ��뱣�ֲ��䣮
���������
�⣨1���ٸ���ͬ�����Ե�Բ�ܽ���Բ�Ľǵ�һ�룬�ߡ�A=135����
���Ż����ԵĽǡ�BOC=270����
���ӻ�BC���Եġ�BOC=90����
��Rt��BOC�У��ɹ��ɶ�����֪BC=![]() =
=![]() .
.
��
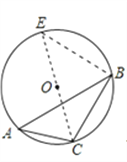
֤������ͼ��ʾ���ӳ�CO��![]() O�ڵ�E������BE��
O�ڵ�E������BE��
���A=��E��
��CEΪ![]() 0��ֱ����
0��ֱ����
���CBE=90����
��sinA=sinE=![]() =
=![]() .
.
��2��
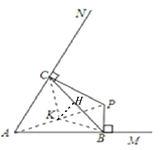
����AP��ȡAP���е�K���ֱ�����CK��BK����KH��BC��BC�ڵ�H��
��BP��AM��CP��AN��K��AP���е㣬
��CK=BK=AK=PK��
���A��B��P��C����KΪԲ�ģ� ![]() APΪ�뾶��Բ�ϣ�
APΪ�뾶��Բ�ϣ�
�ߡ�MAN=60��
���BKC=120��
���KBC=30����
��BC=2��
��BH=CH=![]() ��
��
��cos30��=![]() =
=![]() ��
��
��BK=![]() ��
��
��CK=BK=![]() AP=
AP=![]() ����AP=
����AP=![]() .
.
�������������������У�P��A�����ľ��뱣�ֲ��䣮


 �Ƹ�С״Ԫ�������������ϵ�д�
�Ƹ�С״Ԫ�������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
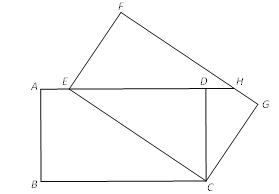
����Ŀ����ͼ��������ABCD�Ƶ�C��ת�õ�����FECG����E��AD�ϣ��ӳ�ED��FG�ڵ�H��
��1����֤����EDC�ա�HFE��
��2������BE��CH��
���ı���BEHC�������������ı��Σ�֤����Ľ��ۣ�
�ڵ�AB��BC�ı�ֵΪ ʱ���ı���BEHCΪ���Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ����������![]() ��
��![]() ��
��![]() �ı�
�ı�![]() ��һ�㣬
��һ�㣬![]() ��ƽ�ƺ�õ�
��ƽ�ƺ�õ�![]() ����
����![]() �Ķ�Ӧ��Ϊ
�Ķ�Ӧ��Ϊ![]() .
.
��1������ƽ�ƺ��![]() ��д����
��д����![]() �����ꣻ
�����ꣻ
��2��![]() �����Ϊ_________________��
�����Ϊ_________________��
��3������![]() ��
��![]() ����һ���㣬
����һ���㣬![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() ֮��Ĺ�ϵʽ���ú�
֮��Ĺ�ϵʽ���ú�![]() ��ʽ�ӱ�ʾ
��ʽ�ӱ�ʾ![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() Ϊ
Ϊ![]() ���ϵ����ߣ�
���ϵ����ߣ�![]() ��
��![]() ����
����![]() ,����
,����![]() .
.
��1����֤���ı���![]() Ϊ���Σ�
����
��2������![]() ����
����![]() ƽ��
ƽ��![]() ��
��![]() ����
����![]() �ij�.
�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �Ķ���
�Ķ���![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ����������ϣ���
����������ϣ���![]() �ڷ���������
�ڷ���������![]() �ĵ�һ�����ڵ�ͼ���ϣ�
�ĵ�һ�����ڵ�ͼ���ϣ�![]() ��
��![]() ������
������![]() ��
��![]() ����Ϸ���������
����Ϸ���������![]() .
.
��1������![]() �����������������ͼ���ϣ����
�����������������ͼ���ϣ����![]() �����ꣻ
�����ꣻ
��2������![]() ��
��![]() ����
����![]() ����Сֵ��
����Сֵ��
��3������![]() ��ƽ����һ�㣬ʹ����
��ƽ����һ�㣬ʹ����![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı��������Σ�������ֱ��д���������������е�
Ϊ������ı��������Σ�������ֱ��д���������������е�![]() ������.
������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�������
��������![]() ������
������![]() ������
������![]() ���һ������Ϊ
���һ������Ϊ![]() ��
��
��1����������![]() �ı���ʽ��
�ı���ʽ��
��2��![]() ��������
��������![]() ��
��![]() �����һ�����㣬��
�����һ�����㣬��![]() ������Ϊ
������Ϊ![]() ������
������![]() ����
����![]() �����Ϊ
�����Ϊ![]() ��
��
����![]() ��ֵ��
��ֵ��
�ڽ�������![]() ����ƽ��
����ƽ��![]() ����λ���õ�������
����λ���õ�������![]() ������
������![]() ʱ��������
ʱ��������![]() ��
��![]() ��ֻ��һ�������㣬��Ϻ�����ͼ����
��ֻ��һ�������㣬��Ϻ�����ͼ����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
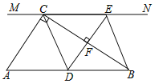
����Ŀ����ͼ����![]() �У�
��![]() ������
������![]() ��ֱ��
��ֱ��![]() ��
��![]() Ϊ
Ϊ![]() ����һ���㣨����
����һ���㣨����![]() ��
��![]() �غϣ�������
�غϣ�������![]() ��
��![]() ����ֱ��
����ֱ��![]() �ڵ�
�ڵ�![]() ������Ϊ
������Ϊ![]() ������
������![]() ��
��![]() .
.
��1����֤��![]() ��
��
��2����![]() �ƶ���
�ƶ���![]() ��ʲôλ��ʱ���ı���
��ʲôλ��ʱ���ı���![]() �����Σ�˵��������ɣ�
�����Σ�˵��������ɣ�
��3������![]() �ƶ���
�ƶ���![]() �е㣬��
�е㣬��![]() �Ĵ�С����ʲô����ʱ���ı���
�Ĵ�С����ʲô����ʱ���ı���![]() �������Σ���˵���������.
�������Σ���˵���������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x1��x2��һԪ���η���2x2��7x+5=0������������һԪ���η��̸���ϵ���Ĺ�ϵ�������и�ʽ��ֵ��
��1��x12x2+x1x22�� ��2����x1��x2��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
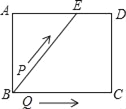
����Ŀ����ͼ������ABCD�У�AB=4cm��AD=5cm����E��AD�ϣ���AE=3cm����P��Qͬʱ�ӵ�B��������P��BE��ED��DC�˶�����Cֹͣ����Q��BC�˶�����Cֹͣ�����ǵ��˶��ٶȶ���1cm/s����P��Q����t�룬��BPQ�����Ϊy cm2����y��t�ĺ�����ϵͼ������ǣ�������
A. 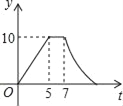 B.
B.  C.
C. 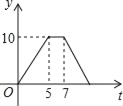 D.
D. 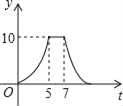
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com