练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】兴趣小组的同学要测量树的高度．在阳光下，一名同学测得一根长为1米的竹竿的影长为0.4米，同时另一名同学测量树的高度时，发现树的影子不全落在地面上，有一部分落在教学楼的第一级台阶上，测得此影长为0.2米，一级台阶高为0.3米，如图所示，若此时落在地面上的影长为4.4米，求树的高度．

    【答案】树的高度为11.8米.

    【解析】

    设树高为h米，根据题意树的高度减去台阶的高所形成的影子长为4.4+0.2（米），然后根据在同一时刻的两个物体，影子，经过物体顶部的太阳光线三者构成的两个直角三角形相似，列出方程，求解即可.

    设树高为h米，

    由题意得，

    则0.4(h－0.3)＝4.6，

    解得：h＝11.8（米）.

    答：树的高度为11.8米.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，某校一幢教学大楼的顶部竖有一块“传承文明，启智求真”的宣传牌CD．小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°，沿山坡向上走到B处测得宣传牌顶部C的仰角为45°．已知山坡AB的坡度i＝1:，AB＝10米，AE＝15米，求这块宣传牌CD的高度．（测角器的高度忽略不计，结果精确到0.1米．参考数据：≈1.414，≈1.732）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某青春党支部在精准扶贫活动中，给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种．已知乙种树苗的价格比甲种树苗贵10元，用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同．

    （1）求甲、乙两种树苗每棵的价格各是多少元？

    （2）在实际帮扶中，他们决定再次购买甲、乙两种树苗共50棵，此时，甲种树苗的售价比第一次购买时降低了10%，乙种树苗的售价不变，如果再次购买两种树苗的总费用不超过1500元，那么他们最多可购买多少棵乙种树苗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对某批乒乓球质量进行随机调查，结果如下表；

    随机抽取的乒乓球数

    10

    20

    50

    100

    200

    500

    1000

    优等品数

    7

    16

    43

    81

    164

    410

    820

    优等频率

    0.7

    0.8

    0.86

    0.81

    0.82

    0.82

    （1）填表格中的空为_______．

    （2）根据上表估计，在这批乒乓球中任取一个球，它为优等品的概率大约是________．（保留两位小数点）

    （3）学校需要500个乒乓球的优等品，那么可以推测出最有可能进这批货的乒乓球个数是多少合适？（结果保留整数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在网格中，每个小正方形的边长都为1，网格中有两个格点、和直线，且长为3．6．

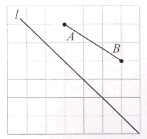
    （1）求作点关于直线的对称点．

    （2）为直线上一动点，在图中标出使的值最小的点，且求出的最小值？

    （3）求周长的最小值？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，有一个圆O和两个正六边形T1，T2． T1的6个顶点都在圆周上，T2的6条边都和圆O相切（我们称T1，T2分别为圆O的内接正六边形和外切正六边形）．

    （1）设T1，T2的边长分别为a，b，圆O的半径为r，求r：a及r：b的值；

    （2）求正六边形T1，T2的面积比S1：S2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，足球场上守门员在O处开出一记手跑高球，球从地面1.4米的A处抛出（A在y轴上），运动员甲在距O点6米的B处发现球在自己头的正上方达到最高点M，距地面3.2米高，球落地点为C点．

    （1）求足球开始抛出到第一次落地时，该抛物线的解析式．

    （2）足球第一次落地点C距守门员多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）甲、乙、丙、丁四人做传球游戏：第一次由甲将球随机传给乙、丙、丁中的某一人，从第二次起，每一次都由持球者将球再随机传给其他三人中的某一人．求第二次传球后球回到甲手里的概率．（请用“画树状图”的方式给出分析过程）

    （2）如果甲跟另外n（n≥2）个人做（1）中同样的游戏，那么，第三次传球后球回到甲手里的概率是 （请直接写出结果）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】美丽的黄河宛如一条玉带穿城而过，沿河两岸的滨河路风情线是兰州最美的景观之一．数学课外实践活动中，小林在南滨河路上的A，B两点处，利用测角仪分别对北岸的一观景亭D进行了测量．如图，测得∠DAC＝45°，∠DBC＝65°.若AB＝132米，求观景亭D到南滨河路AC的距离(结果精确到1米，参考数据：sin65°≈0.91，cos65°≈0.42，tan65°≈2.14)．

    查看答案和解析>>

    同步练习册答案