
【题目】美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14).

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,求树的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
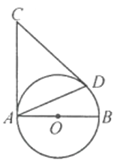
【题目】如图,CA,CD是⊙O的两条切线,切点分别为A,D,AB是⊙O的直径.
⑴ 若∠C=50°,求∠BAD的度数;
⑵ 若AB=AC=4,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的最大值为4,且该抛物线与
的最大值为4,且该抛物线与![]() 轴的交点为
轴的交点为![]() ,顶点为
,顶点为![]() .
.
(1)求该二次函数的解析式及点![]() ,
,![]() 的坐标;
的坐标;
(2)点![]() 是
是![]() 轴上的动点,
轴上的动点,
①求![]() 的最大值及对应的点
的最大值及对应的点![]() 的坐标;
的坐标;
②设![]() 是
是![]() 轴上的动点,若线段
轴上的动点,若线段![]() 与函数
与函数![]() 的图像只有一个公共点,求
的图像只有一个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017重庆A卷第11题)如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米,则此时AB的长约为( )(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
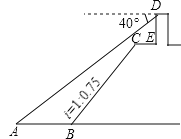
A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F,点M是边AB的一个三等分点.连接MF,则△AOE与△BMF的面积比为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
我们可以通过以下方法求代数式x2+6x+5的最小值.
x2+6x+5=x2+2x3+32﹣32+5=(x+3)2﹣4,
∵(x+3)2≥0
∴当x=﹣3时,x2+6x+5有最小值﹣4.
请根据上述方法,解答下列问题:
(Ⅰ)x2+4x﹣1=x2+2x2+22﹣22﹣1=(x+a)2+b,则ab的值是_____;
(Ⅱ)求证:无论x取何值,代数式x2+2![]() x+7的值都是正数;
x+7的值都是正数;
(Ⅲ)若代数式2x2+kx+7的最小值为2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
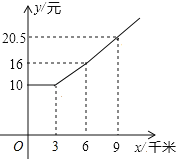
【题目】作为网红城市的重庆,五一节小长假将迎来旅行的高峰,为方便外地游客的出行,重庆市某约车公司推出了一种新型的打车方式,该打车方式的费用收取是按照行驶的路程进行分段计费.小李选用了该打车方式出行,图中折线是小李打车所付车费y(元)与路程x(千米)之间的关系,请根据图象信息,解决下列问题
(1)若小李打车的路程为26千米,则小李所付的车费为 ;
(2)请求出当3≤x≤6时车费y(元)与路程x(千米)之间的关系式;
(3)若小李支付的车费为37元,求小李打车的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=30°,AM是∠BAC的平分线,过M作ME∥BA交AC于E,作MD⊥BA,垂足为D,ME=10cm,则MD=_________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com