
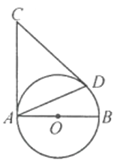
【题目】如图,CA,CD是⊙O的两条切线,切点分别为A,D,AB是⊙O的直径.
⑴ 若∠C=50°,求∠BAD的度数;
⑵ 若AB=AC=4,求AD的长.
【答案】(1)25°;(2) ![]() .
.
【解析】
(1)连接OD,根据四边形内角和定理求得∠AOD,从而得出∠BOD的度数,根据∠BAD=![]() 得出所求;
得出所求;
(2)先根据SAS证明△ACM≌△DCM得出∠CMA=∠CMD=90o,再根据AAS证明△ACM≌△BAD,得出AM=DM=BD,设BD=x,则AD=2x,在△ABD中,![]() +
+![]() =
=![]() ,解方程从而得到AD的长度.
,解方程从而得到AD的长度.
(1)如图所示,连接OD,
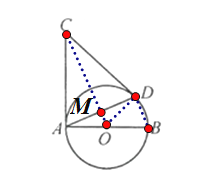
∵CA,CD是⊙O的两条切线,
∴∠OAC=ODC=90o,
又∵∠C=50°,
∴四边形OACD中,∠AOD=(360-90-90-50)°=130°,
∴∠BOD=50°,
∴∠BAD=![]() ;
;
(2)∵CA,CD是⊙O的两条切线,
∴AC=DC,∠ACO=∠DCO,
在△ACM和△DCM中
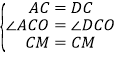
∴△ACM≌△DCM(SAS)
∴∠CMA=∠CMD,AM=DM
∴∠CMA=∠CMD=90o,
∵AB是⊙O的直径
∴∠ADB=∠CMA,
∵∠BAD+∠MAC=90o,∠BAD+∠DBA=90o
∴∠DBA=∠MAC
在△ACM和△BAD中
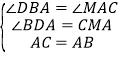
∴△ACM≌△BAD,
∴BD=AM
又∵AM=DM
∴AM=DM=BD
设BD=x,则AD=2x,在△ABD中,![]() +
+![]() =
=![]() ,
,
∴x=![]() ,
,
∴AD=![]() .
.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,足球场上守门员在O处开出一记手跑高球,球从地面1.4米的A处抛出(A在y轴上),运动员甲在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面3.2米高,球落地点为C点.
(1)求足球开始抛出到第一次落地时,该抛物线的解析式.
(2)足球第一次落地点C距守门员多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁中的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人中的某一人.求第二次传球后球回到甲手里的概率.(请用“画树状图”的方式给出分析过程)
(2)如果甲跟另外n(n≥2)个人做(1)中同样的游戏,那么,第三次传球后球回到甲手里的概率是 (请直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在以AB为半径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D
关AC对称,DF⊥DE于点D,并交EC的延长线与点F.下列结论:①CE=CF;②线段EF的最小值为2![]()
③当AD=2时,EF与半圆相切;④当点D从点A运动到点B时,线段EF扫过的面积是16![]() .其中正
.其中正
确的结论()

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
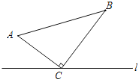
【题目】如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,当一个点到达终点时另一个点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.设运动时间为t秒,则当t=______秒时,△PEC与△QFC全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线经过A![]() ,B
,B![]() ,C
,C![]() 三点.
三点.
(1)求抛物线的解析式。
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线![]() 上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,高AD和BE所在的直线交于点H,且BH=AC,则∠ABC等于( )
A. 45° B. 120° C. 45°或135° D. 45°或120°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com