
【题目】已知二次函数![]() 的最大值为4,且该抛物线与
的最大值为4,且该抛物线与![]() 轴的交点为
轴的交点为![]() ,顶点为
,顶点为![]() .
.
(1)求该二次函数的解析式及点![]() ,
,![]() 的坐标;
的坐标;
(2)点![]() 是
是![]() 轴上的动点,
轴上的动点,
①求![]() 的最大值及对应的点
的最大值及对应的点![]() 的坐标;
的坐标;
②设![]() 是
是![]() 轴上的动点,若线段
轴上的动点,若线段![]() 与函数
与函数![]() 的图像只有一个公共点,求
的图像只有一个公共点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() 点坐标为
点坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() ;(2)①最大值是
;(2)①最大值是![]() ,
,![]() 的坐标为
的坐标为![]() ,②
,②![]() 的取值范围为
的取值范围为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)先利用对称轴公式x=![]() ,计算对称轴,即顶点坐标为(1,4),再将两点代入列二元一次方程组求出解析式;
,计算对称轴,即顶点坐标为(1,4),再将两点代入列二元一次方程组求出解析式;
(2)根据三角形的三边关系:可知P、C、D三点共线时|PC-PD|取得最大值,求出直线CD与x轴的交点坐标,就是此时点P的坐标;
(3)先把函数中的绝对值化去,可知![]() ,此函数是两个二次函数的一部分,分三种情况进行计算:①当线段PQ过点(0,3),即点Q与点C重合时,两图象有一个公共点,当线段PQ过点(3,0),即点P与点(3,0)重合时,两函数有两个公共点,写出t的取值;②线段PQ与当函数y=a|x|2-2a|x|+c(x≥0)时有一个公共点时,求t的值;③当线段PQ过点(-3,0),即点P与点(-3,0)重合时,线段PQ与当函数y=a|x|2-2a|x|+c(x<0)时也有一个公共点,则当t≤-3时,都满足条件;综合以上结论,得出t的取值.
,此函数是两个二次函数的一部分,分三种情况进行计算:①当线段PQ过点(0,3),即点Q与点C重合时,两图象有一个公共点,当线段PQ过点(3,0),即点P与点(3,0)重合时,两函数有两个公共点,写出t的取值;②线段PQ与当函数y=a|x|2-2a|x|+c(x≥0)时有一个公共点时,求t的值;③当线段PQ过点(-3,0),即点P与点(-3,0)重合时,线段PQ与当函数y=a|x|2-2a|x|+c(x<0)时也有一个公共点,则当t≤-3时,都满足条件;综合以上结论,得出t的取值.
解:(1)∵![]() ,
,
∴![]() 的对称轴为
的对称轴为![]() .
.
∵![]() 人最大值为4,
人最大值为4,
∴抛物线过点![]() .
.
得![]() ,
,
解得![]() .
.
∴该二次函数的解析式为![]() .
.
![]() 点坐标为
点坐标为![]() ,顶点
,顶点![]() 的坐标为
的坐标为![]() .
.
(2)①∵![]() ,
,
∴当![]() 三点在一条直线上时,
三点在一条直线上时,![]() 取得最大值.
取得最大值.
连接![]() 并延长交
并延长交![]() 轴于点
轴于点![]() ,
,![]() .
.
∴![]() 的最大值是
的最大值是![]() .
.
易得直线![]() 的方程为
的方程为![]() .
.
把![]() 代入,得
代入,得![]() .
.
∴此时对应的点![]() 的坐标为
的坐标为![]() .
.
②![]() 的解析式可化为
的解析式可化为![]()
设线段![]() 所在直线的方程为
所在直线的方程为![]() ,将
,将![]() ,
,![]() 的坐标代入,可得线段
的坐标代入,可得线段![]() 所在直线的方程为
所在直线的方程为![]() .
.
(1)当线段![]() 过点
过点![]() ,即点
,即点![]() 与点
与点![]() 重合时,线段
重合时,线段![]() 与函数
与函数![]() 的图像只有一个公共点,此时
的图像只有一个公共点,此时![]() .
.
∴当![]() 时,线段
时,线段![]() 与函数
与函数![]() 的图像只有一个公共点.
的图像只有一个公共点.
(2)当线段![]() 过点
过点![]() ,即点
,即点![]() 与点
与点![]() 重合时,线段
重合时,线段![]() 与函数
与函数![]() 的图像只有一个公共点,此时
的图像只有一个公共点,此时![]() .
.
当线段![]() 过点
过点![]() ,即点
,即点![]() 与点
与点![]() 重合时,
重合时,![]() ,此时线段
,此时线段![]() 与函数
与函数![]() 的图像有两个公共点.
的图像有两个公共点.
所以当![]() 时,线段
时,线段![]() 与函数
与函数![]() 的图像只有一个公共点.
的图像只有一个公共点.
(3)将![]() 带入
带入![]() ,并整理,得
,并整理,得![]() .
.
![]() .
.
令![]() ,解得
,解得![]() .
.
∴当![]() 时,线段
时,线段![]() 与函数
与函数![]() 的图像只有一个公共点.
的图像只有一个公共点.
综上所述,![]() 的取值范围为
的取值范围为![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】对某批乒乓球质量进行随机调查,结果如下表;
随机抽取的乒乓球数 | 10 | 20 | 50 | 100 | 200 | 500 | 1000 |
优等品数 | 7 | 16 | 43 | 81 | 164 | 410 | 820 |
优等频率 | 0.7 | 0.8 | 0.86 | 0.81 | 0.82 | 0.82 |
(1)填表格中的空为_______.
(2)根据上表估计,在这批乒乓球中任取一个球,它为优等品的概率大约是________.(保留两位小数点)
(3)学校需要500个乒乓球的优等品,那么可以推测出最有可能进这批货的乒乓球个数是多少合适?(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)甲、乙、丙、丁四人做传球游戏:第一次由甲将球随机传给乙、丙、丁中的某一人,从第二次起,每一次都由持球者将球再随机传给其他三人中的某一人.求第二次传球后球回到甲手里的概率.(请用“画树状图”的方式给出分析过程)
(2)如果甲跟另外n(n≥2)个人做(1)中同样的游戏,那么,第三次传球后球回到甲手里的概率是 (请直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
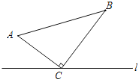
【题目】如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,当一个点到达终点时另一个点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.设运动时间为t秒,则当t=______秒时,△PEC与△QFC全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线经过A![]() ,B
,B![]() ,C
,C![]() 三点.
三点.
(1)求抛物线的解析式。
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线![]() 上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )

A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】清明小长假是广大游客走出家门放松心情、感受祖国大好河山的好时机,为丰富游客出行体验,小长假前夕,遵义市启动了2018年“醉美遵义,四季主题游”之春季踏青赏花游。三天假期,遵义市共接待游客230.11万人次,实现旅游综合收入12.66亿元,把12.66亿用科学计数法表示为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,线段
,线段![]() ,若点A在y轴上滑动,点B随着线段AB在射线x轴上滑动,(A、B与O不重合),Rt△AOB的内切⊙K分别与OA、OB、AB切于E、F、P.
,若点A在y轴上滑动,点B随着线段AB在射线x轴上滑动,(A、B与O不重合),Rt△AOB的内切⊙K分别与OA、OB、AB切于E、F、P.
(1)在上述变化过程中:Rt△AOB的周长,⊙K的半径,△AOB外接圆半径,这几个量中不会发生变化的是什么?并简要说明理由;
(2)当![]() 时,求⊙K的半径r;
时,求⊙K的半径r;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com