
【题目】如图,已知![]() ,线段
,线段![]() ,若点A在y轴上滑动,点B随着线段AB在射线x轴上滑动,(A、B与O不重合),Rt△AOB的内切⊙K分别与OA、OB、AB切于E、F、P.
,若点A在y轴上滑动,点B随着线段AB在射线x轴上滑动,(A、B与O不重合),Rt△AOB的内切⊙K分别与OA、OB、AB切于E、F、P.
(1)在上述变化过程中:Rt△AOB的周长,⊙K的半径,△AOB外接圆半径,这几个量中不会发生变化的是什么?并简要说明理由;
(2)当![]() 时,求⊙K的半径r;
时,求⊙K的半径r;

【答案】 (1)△AOB的外接圆半径(2)![]()
【解析】
(1)根据直角三角形的性质,斜边上的中线等于斜边的一半,AB的长不变,即△AOB的外接圆半径不变,即可得出答案;
(2)设⊙K的半径为r,连EK、KF,则四边形EOFK是正方形,根据切线长定理,即可求得⊙K的半径 r的值;
(1)不会发生变化的是△AOB的外接圆半径,
∵![]() ,
,
∴AB是△AOB的外接圆的直径,
∵AB的长不变,
即△AOB的外接圆半径不变;
(2)设⊙K的半径为r,⊙K与y轴、x轴相切于E、F、P,连EK、KF,
∴![]() ,
,
∴四边形EOFK是矩形,又![]() ,
,
∴四边形EOFK是正方形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() (不符合题意),或
(不符合题意),或![]() ,
,
∴⊙K的半径r为2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的最大值为4,且该抛物线与
的最大值为4,且该抛物线与![]() 轴的交点为
轴的交点为![]() ,顶点为
,顶点为![]() .
.
(1)求该二次函数的解析式及点![]() ,
,![]() 的坐标;
的坐标;
(2)点![]() 是
是![]() 轴上的动点,
轴上的动点,
①求![]() 的最大值及对应的点
的最大值及对应的点![]() 的坐标;
的坐标;
②设![]() 是
是![]() 轴上的动点,若线段
轴上的动点,若线段![]() 与函数
与函数![]() 的图像只有一个公共点,求
的图像只有一个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
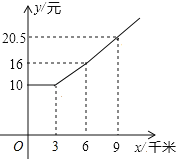
【题目】作为网红城市的重庆,五一节小长假将迎来旅行的高峰,为方便外地游客的出行,重庆市某约车公司推出了一种新型的打车方式,该打车方式的费用收取是按照行驶的路程进行分段计费.小李选用了该打车方式出行,图中折线是小李打车所付车费y(元)与路程x(千米)之间的关系,请根据图象信息,解决下列问题
(1)若小李打车的路程为26千米,则小李所付的车费为 ;
(2)请求出当3≤x≤6时车费y(元)与路程x(千米)之间的关系式;
(3)若小李支付的车费为37元,求小李打车的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=30°,P是OA上的一点,OP=24cm,以r为半径作⊙P.

(1)若r=12cm,试判断⊙P与OB位置关系;
(2)若⊙P与OB相离,试求出r需满足的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知命题“等腰三角形两腰上的高线长相等”
(1)请写出该命题的逆命题;
(2)判断(1)中命题的真假,并画出图形,补充已知,求证,及证明过程.
图形:
已知:在△ABC中,CD⊥AB,BE⊥AC,且______.
求证:______.
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,M是弦AB的中点,过点B作⊙O的切线,与OM延长线交于点C.

(1)求证:∠A=∠C;
(2)若OA=5,AB=8,求线段OC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAC=30°,AM是∠BAC的平分线,过M作ME∥BA交AC于E,作MD⊥BA,垂足为D,ME=10cm,则MD=_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:有一个直角三角形ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到离A的距离等于___________时,ΔABC和ΔPQA全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD在平面直角坐标系中,点A(1,8),B(1,6),C(7,6),点X,Y分别在x,y轴上.
(1)请直接写出D点的坐标 ;
(2)连接OB、OD,OD交BC于点E,∠BOY的平分线和∠BEO的平分线交于点F,若∠BOE=n,求∠OFE的度数.
(3)若长方形ABCD以每秒![]() 个单位的速度向下运动,设运动时间为t秒,问在第一象限内是否存在某一时刻t,使△OBD的面积等于长方形ABCD的面积的
个单位的速度向下运动,设运动时间为t秒,问在第一象限内是否存在某一时刻t,使△OBD的面积等于长方形ABCD的面积的![]() ?若存在,请求出t的值,若不存在,请说明理由。
?若存在,请求出t的值,若不存在,请说明理由。


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com