
【题目】已知∠AOB=30°,P是OA上的一点,OP=24cm,以r为半径作⊙P.

(1)若r=12cm,试判断⊙P与OB位置关系;
(2)若⊙P与OB相离,试求出r需满足的条件.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,当一个点到达终点时另一个点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.设运动时间为t秒,则当t=______秒时,△PEC与△QFC全等.
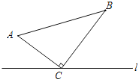
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】清明小长假是广大游客走出家门放松心情、感受祖国大好河山的好时机,为丰富游客出行体验,小长假前夕,遵义市启动了2018年“醉美遵义,四季主题游”之春季踏青赏花游。三天假期,遵义市共接待游客230.11万人次,实现旅游综合收入12.66亿元,把12.66亿用科学计数法表示为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数y=x+|x﹣2|的图象与性质
小明根据学习函数的经验,对函数y=x+|x﹣2|的图象与性质进行了探究
下面是小明的探究过程,请补充完成:
(1)化简函数解析式,当x≥2时,y= ;当x<2时,y= ;
(2)根据(1)中的结果,请在图1的坐标系中画出函数y=x+|x﹣2|的图象;
(3)结合函数的图象,写出该函数的一条性质: ;
(4)结合画出的函数图象,利用图2解决问题,若关于x的方程ax+1=x+|x﹣2|有两个实数根,直接写出实数a的取值范围: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,高AD和BE所在的直线交于点H,且BH=AC,则∠ABC等于( )
A. 45° B. 120° C. 45°或135° D. 45°或120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF
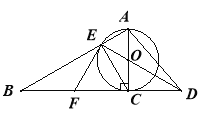
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,线段
,线段![]() ,若点A在y轴上滑动,点B随着线段AB在射线x轴上滑动,(A、B与O不重合),Rt△AOB的内切⊙K分别与OA、OB、AB切于E、F、P.
,若点A在y轴上滑动,点B随着线段AB在射线x轴上滑动,(A、B与O不重合),Rt△AOB的内切⊙K分别与OA、OB、AB切于E、F、P.
(1)在上述变化过程中:Rt△AOB的周长,⊙K的半径,△AOB外接圆半径,这几个量中不会发生变化的是什么?并简要说明理由;
(2)当![]() 时,求⊙K的半径r;
时,求⊙K的半径r;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=70°,∠BAC的平分线与AB的垂直平分线交于点O,点E、F分别在BC、AC上,点C沿EF折叠后与点O重合,则∠BEO的度数是( )
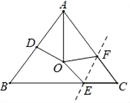
A. 20° B. 35° C. 40° D. 55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,∠ADC的平分线与AB交于E,点F在DE的延长线上,∠BFE=90°,连接AF、CF,CF与AB交于G.有以下结论:
①AE=BC
②AF=CF
③BF2=FGFC
④EGAE=BGAB
其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com