
【题目】有这样一个问题:探究函数y=x+|x﹣2|的图象与性质
小明根据学习函数的经验,对函数y=x+|x﹣2|的图象与性质进行了探究
下面是小明的探究过程,请补充完成:
(1)化简函数解析式,当x≥2时,y= ;当x<2时,y= ;
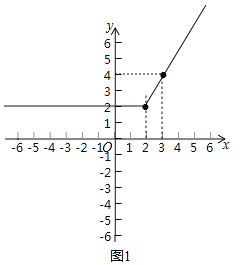
(2)根据(1)中的结果,请在图1的坐标系中画出函数y=x+|x﹣2|的图象;
(3)结合函数的图象,写出该函数的一条性质: ;
(4)结合画出的函数图象,利用图2解决问题,若关于x的方程ax+1=x+|x﹣2|有两个实数根,直接写出实数a的取值范围: .

【答案】(1)y=2x﹣2; y=2;(2)详见解析;(3)当x>2时,y随x的增大而增大;(4)0.5<a<2.
【解析】
(1)根据题目中的函数解析式,可以分别写出x≥2和x<2时的函数解析式;
(2)根据(1)中的结果,可以在图1的坐标系中画出函数y=x+|x﹣2|的图象;
(3)根据(1)中的函数图象,可以写出函数y=x+|x﹣2|的一条性质,本题答案不唯一,只要符合题意即可;
(4)根据一次函数与方程的关系,可以得到关于x的方程ax+1=x+|x﹣2|有两个实数根时,a的取值范围.
(1)当x≥2时,y=x+|x﹣2|=x+x﹣2=2x﹣2,
当x<2时,y=x+|x﹣2|=x+2﹣x=2,
故答案为:2x﹣2,2;
(2)当x≥2时,y=2x﹣2过点(2,2),(3,4),
函数y=x+|x﹣2|的图象如图1所示;
(3)由图象可知,
当x>2时,y随x的增大而增大,
故答案为:当x>2时,y随x的增大而增大;
(4)∵y=ax+1的函数图象一定过点(0,1)
∴当y=ax+1中的a=2时,直线y=ax+1与直线y=x+|x﹣2|有一个交点,
当a≥2或a<0时,y=ax+1与y=x+|x﹣2|有一个交点,
当直线y=ax+1过点(2,2)时,2=2a+1,得a=0.5,故当0≤a<0.5时,y=ax+1与y=x+|x﹣2|没有交点,当a=0.5时,y=ax+1与y=x+|x﹣2|有一个交点,
由上可得,关于x的方程ax+1=x+|x﹣2|有两个实数根,实数a的取值范围是:0.5<a<2,
故答案为:0.5<a<2.



 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】已知M(x,y)是平面直角坐标系xOy中的点,其中x是从l、2、3三个数中任取的一个数,y是从l、2、3、4四个数中任取的一个数 .
(l)计算由x、y确定的点M(x,y)在函数y= -x+5的图象上的概率;
(2)小明和小红约定做一个游戏,其规则为:若x、y满足xy>6则小明胜;若x、y满足xy<6则小红胜,这个游戏公平吗?说明理由. 若不公平,请写出公平的游戏规则;
(3)定义“点M(x,y)在直线x+y=n上”为事件A(2≤n≤7,n为整数),则当A的概率最大时,n的所有可能的值为 .(不需要解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F,点M是边AB的一个三等分点.连接MF,则△AOE与△BMF的面积比为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形![]() 恰好被分割成3个边长为
恰好被分割成3个边长为![]() 的大正方形和4个边长为
的大正方形和4个边长为![]() 的小正方形,取1个大正方形和2个小正方形将两个小正方形放置在大正方形中(如图2所示).若图2中阴影都分的面积比四边形
的小正方形,取1个大正方形和2个小正方形将两个小正方形放置在大正方形中(如图2所示).若图2中阴影都分的面积比四边形![]() 的面积小80,则边长为
的面积小80,则边长为![]() 的正方形面积是________.
的正方形面积是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
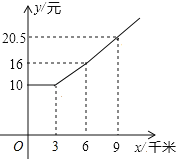
【题目】作为网红城市的重庆,五一节小长假将迎来旅行的高峰,为方便外地游客的出行,重庆市某约车公司推出了一种新型的打车方式,该打车方式的费用收取是按照行驶的路程进行分段计费.小李选用了该打车方式出行,图中折线是小李打车所付车费y(元)与路程x(千米)之间的关系,请根据图象信息,解决下列问题
(1)若小李打车的路程为26千米,则小李所付的车费为 ;
(2)请求出当3≤x≤6时车费y(元)与路程x(千米)之间的关系式;
(3)若小李支付的车费为37元,求小李打车的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列一定是一元二次方程的有( )
(1)(a-1)x+bx+c=0(a,b,c是实数);(2)2x+![]() +3=0;(3)(1-2x)(3-x)=2x+1;(4)x+2x-y=0;(5)
+3=0;(3)(1-2x)(3-x)=2x+1;(4)x+2x-y=0;(5)![]() x-8=
x-8=![]() x
x
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=30°,P是OA上的一点,OP=24cm,以r为半径作⊙P.

(1)若r=12cm,试判断⊙P与OB位置关系;
(2)若⊙P与OB相离,试求出r需满足的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,M是弦AB的中点,过点B作⊙O的切线,与OM延长线交于点C.

(1)求证:∠A=∠C;
(2)若OA=5,AB=8,求线段OC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境:在数学活动课上,老师出示了这样一个问题:如图1,在矩形ABCD中,AD=2AB,E是AB延长线上一点,且BE=AB,连接DE,交BC于点M,以DE为一边在DE的左下方作正方形DEFG,连接AM.试判断线段AM与DE的位置关系.
探究展示:勤奋小组发现,AM垂直平分DE,并展示了如下的证明方法:
证明:∵BE=AB,∴AE=2AB.
∵AD=2AB,∴AD=AE.
∵四边形ABCD是矩形,∴AD∥BC.
∴![]() .(依据1)
.(依据1)
∵BE=AB,∴![]() .∴EM=DM.
.∴EM=DM.
即AM是△ADE的DE边上的中线,
又∵AD=AE,∴AM⊥DE.(依据2)
∴AM垂直平分DE.
反思交流:
(1)①上述证明过程中的“依据1”“依据2”分别是指什么?
②试判断图1中的点A是否在线段GF的垂直平分线上,请直接回答,不必证明;
(2)创新小组受到勤奋小组的启发,继续进行探究,如图2,连接CE,以CE为一边在CE的左下方作正方形CEFG,发现点G在线段BC的垂直平分线上,请你给出证明;
探索发现:
(3)如图3,连接CE,以CE为一边在CE的右上方作正方形CEFG,可以发现点C,点B都在线段AE的垂直平分线上,除此之外,请观察矩形ABCD和正方形CEFG的顶点与边,你还能发现哪个顶点在哪条边的垂直平分线上,请写出一个你发现的结论,并加以证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com