
【题目】如图,在⊙O中,M是弦AB的中点,过点B作⊙O的切线,与OM延长线交于点C.

(1)求证:∠A=∠C;
(2)若OA=5,AB=8,求线段OC的长.
【答案】(1)见解析(2)![]()
【解析】
(1)连接OB,由OA=OB,可知∠A=∠OBM,又M是AB中点,利用等腰三角形三线合一定理可知OC⊥AB,即可得∠C+∠CBM=90°,而BC是切线可得∠OBM+∠CBM=90°,即∠A+∠CBM=90°,利用等角的余角相等可得∠A=∠C;
(2)由(1)得∠C=∠OBM,∠OBC=∠OMB=90°,易证△OMB∽△OBC,即可得OB:OC=OM:OB,而BM=![]() AB=4,根据勾股定理可求OM,进而即可求出OC的长.
AB=4,根据勾股定理可求OM,进而即可求出OC的长.
(1)证明:连接OB,
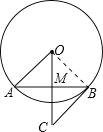
∵BC是切线,
∴∠OBC=90°,
∴∠OBM+∠CBM=90°,
∵OA=OB,
∴∠A=∠OBM,
∵M是AB的中点,
∴OM⊥AB.
∴∠C+∠CBM=90°,
∴∠C=∠OBM,
∴∠A=∠C;
(2)∵∠C=∠OBM,∠OBC=∠OMB=90°,
∴△OMB∽△OBC,
∴![]() =
=![]() ,
,
又∵BM=![]() AB=4,
AB=4,
∴OM=52-42=3,
∴OC=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )

A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数y=x+|x﹣2|的图象与性质
小明根据学习函数的经验,对函数y=x+|x﹣2|的图象与性质进行了探究
下面是小明的探究过程,请补充完成:
(1)化简函数解析式,当x≥2时,y= ;当x<2时,y= ;
(2)根据(1)中的结果,请在图1的坐标系中画出函数y=x+|x﹣2|的图象;
(3)结合函数的图象,写出该函数的一条性质: ;
(4)结合画出的函数图象,利用图2解决问题,若关于x的方程ax+1=x+|x﹣2|有两个实数根,直接写出实数a的取值范围: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF
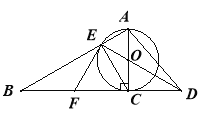
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,线段
,线段![]() ,若点A在y轴上滑动,点B随着线段AB在射线x轴上滑动,(A、B与O不重合),Rt△AOB的内切⊙K分别与OA、OB、AB切于E、F、P.
,若点A在y轴上滑动,点B随着线段AB在射线x轴上滑动,(A、B与O不重合),Rt△AOB的内切⊙K分别与OA、OB、AB切于E、F、P.
(1)在上述变化过程中:Rt△AOB的周长,⊙K的半径,△AOB外接圆半径,这几个量中不会发生变化的是什么?并简要说明理由;
(2)当![]() 时,求⊙K的半径r;
时,求⊙K的半径r;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售A、B两种品牌的教学设备,这两种教学设备的进价和售价如下表所示:
教学设备 | A | B |
进价(万元/套) | 3 | 2.4 |
售价(万元/套) | 3.3 | 2.8 |
该商场计划购进两种教学设备若干套,共需132万元,全部销售后可获毛利润18万元.
(1)该商场计划购进A、B两种品牌的教学设备各多少套?
(2)通过市场调查,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少数量的1.5倍.若用于购进这两种教学设备的总资金不超过138万元,则A种设备购进数量最多减少多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=70°,∠BAC的平分线与AB的垂直平分线交于点O,点E、F分别在BC、AC上,点C沿EF折叠后与点O重合,则∠BEO的度数是( )
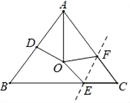
A. 20° B. 35° C. 40° D. 55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=54°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为 度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com