
【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF
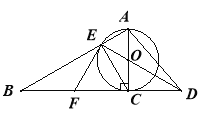
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长。
【答案】(2)![]()
【解析】
试题(1)连接FO,可根据三角形中位线的性质可判断易证OF∥AB,然后根据直径所对的圆周角是直角,可得CE⊥AE,进而知OF⊥CE,然后根据垂径定理可得∠FEC=∠FCE,∠0EC=∠0CE,再通过Rt△ABC可知∠0EC+∠FEC=90°,因此可证FE为⊙O的切线;
(2)根据⊙O的半径为3,可知AO=CO=EO=3,再由∠EAC=60°可证得∠COD=∠EOA=60°,在Rt△OCD中,∠COD=60°,OC=3,可由勾股定理求得CD=3![]() ,最后根据Rt△ACD,用勾股定理求得结果.
,最后根据Rt△ACD,用勾股定理求得结果.
试题解析:
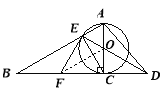
证明:(1)连接FO
易证OF∥AB
∵AC⊙O的直径
∴CE⊥AE
∵OF∥AB
∴OF⊥CE
∴OF所在直线垂直平分CE
∴FC=FE,OE=OC
∴∠FEC=∠FCE,∠0EC=∠0CE
∵Rt△ABC
∴∠ACB=90°
即:∠0CE+∠FCE=90°
∴∠0EC+∠FEC=90°
即:∠FEO=90°
∴FE为⊙O的切线
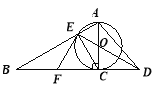
(2)∵⊙O的半径为3
∴AO=CO=EO=3
∵∠EAC=60°,OA=OE
∴∠EOA=60°
∴∠COD=∠EOA=60°
∵在Rt△OCD中,∠COD=60°,OC=3
∴CD=![]()
∵在Rt△ACD中,∠ACD=90°,
CD=![]() ,AC=6
,AC=6
∴AD=![]()


科目:初中数学 来源: 题型:
【题目】如图1,长方形![]() 恰好被分割成3个边长为
恰好被分割成3个边长为![]() 的大正方形和4个边长为
的大正方形和4个边长为![]() 的小正方形,取1个大正方形和2个小正方形将两个小正方形放置在大正方形中(如图2所示).若图2中阴影都分的面积比四边形
的小正方形,取1个大正方形和2个小正方形将两个小正方形放置在大正方形中(如图2所示).若图2中阴影都分的面积比四边形![]() 的面积小80,则边长为
的面积小80,则边长为![]() 的正方形面积是________.
的正方形面积是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列一定是一元二次方程的有( )
(1)(a-1)x+bx+c=0(a,b,c是实数);(2)2x+![]() +3=0;(3)(1-2x)(3-x)=2x+1;(4)x+2x-y=0;(5)
+3=0;(3)(1-2x)(3-x)=2x+1;(4)x+2x-y=0;(5)![]() x-8=
x-8=![]() x
x
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=30°,P是OA上的一点,OP=24cm,以r为半径作⊙P.

(1)若r=12cm,试判断⊙P与OB位置关系;
(2)若⊙P与OB相离,试求出r需满足的条件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据直尺和三角尺的实物摆放图,解决下列问题.



(1)如图1,是我们学过的用直尺和三角尺画平行线的方法的示意图,画图的原理是__________;
(2)如图2,图中互余的角有________________,若要使直尺的边缘DE与三角尺的AB边平行,则应满足_________(填角相等);
(3)如图3,若BC∥GH,试判断AC和FG的位置关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,M是弦AB的中点,过点B作⊙O的切线,与OM延长线交于点C.

(1)求证:∠A=∠C;
(2)若OA=5,AB=8,求线段OC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中国梦”关乎每个人的幸福生活,为进一步感知我们身边的幸福,展现成都人追梦的风采,我市某校开展了以“梦想中国,逐梦成都”为主题的摄影大赛,要求参赛学生每人交一件作品.现将参赛的50件作品的成绩(单位:分)进行统计如下:
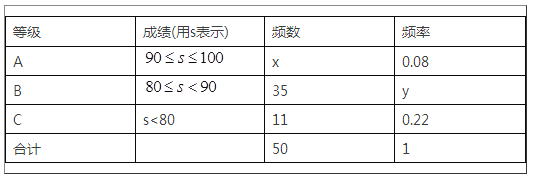
请根据上表提供的信息,解答下列问题:
(1)表中x的值为________,y的值为________;
(2)将本次参赛作品获得A等级的学生依次用A1,A2,A3,…表示,现该校决定从本次参赛作品获得A等级的学生中,随机抽取两名学生谈谈他们的参赛体会,请用树状图或列表法求恰好抽到学生A1和A2的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若△ABC内一点P满足∠PAC=∠PCB=∠PBA,则称点P为△ABC的布罗卡尔点,三角形的布罗卡尔点是法国数学家和数学教育家克雷尔首次发现,后来被数学爱好者法国军官布罗卡尔重新发现,并用他的名字命名,布罗卡尔点的再次发现,引发了研究“三角形几何”的热潮.已知△ABC中,CA=CB,∠ACB=120°,P为△ABC的布罗卡尔点,若PA=![]() ,则PB+PC=_____.
,则PB+PC=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com