
【题目】已知二次函数![]() (
(![]() 为常数),当自变量
为常数),当自变量![]() 的值满足
的值满足![]() 时,与其对应的函数值
时,与其对应的函数值![]() 的最小值为4,则
的最小值为4,则![]() 的值为( )
的值为( )
A.1或-5B.-5或3C.-3或1D.-3或5
【答案】D
【解析】
根据函数二次函数![]() (
(![]() 为常数)可得函数对称轴为
为常数)可得函数对称轴为![]() ,由自变量
,由自变量![]() 的值满足
的值满足![]() 时,其对应的函数值
时,其对应的函数值![]() 的最小值为4,再对h的大小进行分类讨论,当
的最小值为4,再对h的大小进行分类讨论,当![]() 时,自变量
时,自变量![]() 的值满足
的值满足![]() 时,y随x的增大而减小,当x=3时,y取得最小值为
时,y随x的增大而减小,当x=3时,y取得最小值为
![]() ,可解得h的值,并且注意检验h要满足
,可解得h的值,并且注意检验h要满足![]() ;当
;当![]() 时,自变量
时,自变量![]() 的值满足
的值满足![]() 时,y随x的增大而增大,当
时,y随x的增大而增大,当![]() 时,y取得最小值为
时,y取得最小值为![]() ,可解得h的值,并且注意检验h要满足
,可解得h的值,并且注意检验h要满足![]() ,即可得出答案.
,即可得出答案.
解:∵二次函数![]() (
(![]() 为常数),
为常数),
∴函数对称轴为![]() ;
;
∵函数的二次项系数a=1,
∴函数开口向上,
当![]() 时,
时,![]() 的值满足
的值满足![]() 在对称轴的左侧,y随x的增大而减小,
在对称轴的左侧,y随x的增大而减小,
∴当x=3时,y取得最小值,此时![]() ,解得:
,解得:![]()
∵![]() ,
,
∴![]() 舍去,
舍去,![]() ;
;
当![]() 时,
时,![]() 的值满足
的值满足![]() 在对称轴的右侧,y随x的增大而增大,
在对称轴的右侧,y随x的增大而增大,
∴当![]() 时,y取得最小值,此时
时,y取得最小值,此时![]() ,解得:
,解得:![]()
∵![]() ,
,
∴![]() 舍去,
舍去,![]() ;
;
综上所述,![]() 或
或![]() ;
;
故答案为D.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,小辉从家(点0)出发,沿着等腰三角形A0B的边0A-AB-B0的路径去匀匀速散步,其中0A=0B。设小辉距家(点0)的距离为S,散步的时间为t,则下列图形中能大致刻画S与t之间函数关系的图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠ACB=90°,AC=BC,AE 是 BC 边的中线,过点C 作 CF⊥AE,垂足为点 F,过点 B 作 BD⊥BC 交 CF 的延长线于点 D.
(1)试证明:AE=CD;
(2)若 AC=12cm,求线段 BD 的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠C=90°,AC<BC,D为BC上一点,且到A,B两点的距离相等.
(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=33°,则∠CAD= °.

查看答案和解析>>
科目:初中数学 来源: 题型:
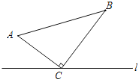
【题目】如图,△ABC中,∠ACB=90°,AC=6cm,BC=8cm.点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1cm和3cm的运动速度同时开始运动,当一个点到达终点时另一个点也停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.设运动时间为t秒,则当t=______秒时,△PEC与△QFC全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx+b与抛物线y=![]() x2交于A(x1,y1),B(x2,y2)两点,当OA⊥OB时,直线AB恒过一个定点,该定点坐标为___________.
x2交于A(x1,y1),B(x2,y2)两点,当OA⊥OB时,直线AB恒过一个定点,该定点坐标为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )

A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据要求,解答下列问题:
(1)①方程x2﹣x﹣2=0的解为 ;
②方程x2﹣2x﹣3=0的解为 ;
③方程x2﹣3x﹣4=0的解为 ;
…
(2)根据以上方程特征及其解的特征,请猜想:
①方程x2﹣9x﹣10=0的解为 ;
②请用配方法解方程x2﹣9x﹣10=0,以验证猜想结论的正确性.
(3)应用:关于x的方程 的解为x1=﹣1,x2=n+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF
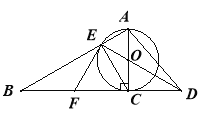
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com